Planar Graphs

A planar graph is a graph that can be depicted on a flat plane in such a way that its edges intersect only at their vertices.

This arrangement allows for a layout where no two edges overlap, maintaining a clear separation between them.

For every connected finite planar graph, Euler's formula is a cornerstone:

$$ V-E+F=2 $$

Here, V represents the number of vertices, E the number of edges, and F the count of faces—areas enclosed by edges, including the space outside the graph.

This formula is pivotal in assessing the planarity of a graph.

Example

Consider a planar graph with 5 vertices and 7 edges.

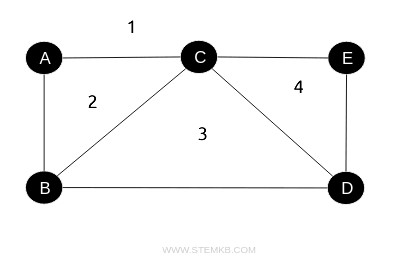
It is composed of F=4 faces, which include three internal areas and one external area.

$$ V-E+F=2 $$

$$ 5-7+4=2 $$

$$ 2 = 2 $$

The graph fulfills Euler's formula, affirming its planarity.

Example 2

This graph is similar to the one before but it's not a planar graph because two edges, AD and BC, intersect.

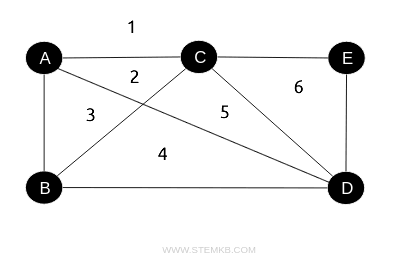
In this case, Euler's formula does not hold, since we have V=5 vertices, E=8 edges, and F=6 faces.

$$ V-E+F=2 $$

$$ 5-8+6=3 $$

But, $$ 3 ≠ 2 $$