Subgraphs

In graph theory, a subgraph is derived from a parent graph G, including only a subset of G's nodes and edges.

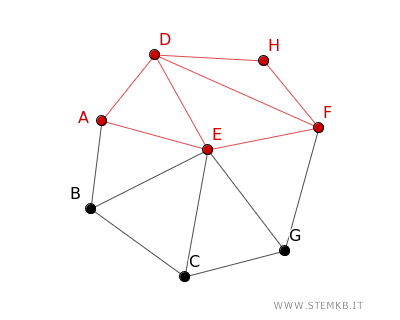
To put it simply, if G is a graph, a subgraph of G, denoted as S, is composed of nodes and edges where each node in S is found in G, and every edge in S connects nodes also in G.

This essentially means a subgraph captures a specific segment of the broader graph.

Subgraphs come in various forms, such as induced subgraphs, sparse subgraphs, and complete subgraphs, each serving different purposes and offering unique insights.

Take, for example, an induced subgraph. It's generated by selecting a subset of nodes from G and all edges connecting these nodes in G, proving to be an invaluable tool for examining graph's local characteristics.

Subgraphs are incredibly useful in a wide array of practical situations, enabling the simplification of complex problems or the discovery of important patterns within vast networks.

An Illustrative Example

Imagine a graph G that maps out the cities of a country with cities as nodes and roads as edges between them.

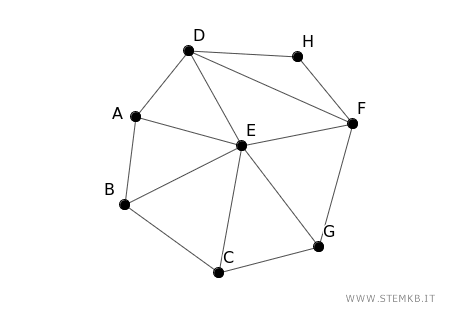
The vertices V(G) and edges E(G) of graph G are listed as follows:

$$ V(G) = \{ A,B,C,D,E,F,G,H \} $$

$$ E(G) = \{ AB, AD, BC, CG, EG, EF, ED, DF, DH, FH  \} $$

Let's say we're interested in focusing on a particular region, like the northern part of the country.

By selecting cities in the north and the roads connecting them, we form a subgraph S from the original graph.

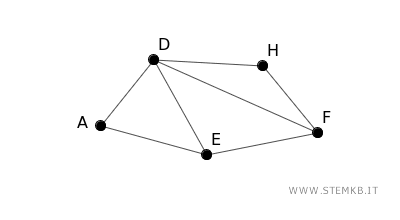
This subgraph has fewer nodes and edges than the complete graph but preserves the relationship dynamics among the chosen cities.

$$ V(S) = \{ A, D, E, F, H \} $$

$$ E(S) = \{ AE, AD, ED, EF, DF, DH, FH  \} $$

The vertices set V(S) and edges set E(G) of the subgraph are subsets of the original graph, indicating:

$$ V(S) \subseteq V(G) $$

$$ E(S) \subseteq E(G) $$

This scenario showcases how subgraphs can streamline the analysis of specific segments within larger networks, maintaining essential connectivity information without overwhelming detail.