Complete Graph

A graph $ G = (V, E) $ is called a complete graph if, for every pair of vertices $ u, v \in V $, there is an edge $ (u, v) \in E $.

In other words, a complete graph is one where every pair of vertices is connected by an edge.

If the graph is directed, each pair of vertices $ (u, v) $ is connected by edges in both directions.

Imagine you're at a party where you know everyone: that's like a complete graph. Everyone is talking to everyone else, without exception!

What are complete graphs used for?

Complete graphs are used in optimization problems, such as the traveling salesman problem, where the goal is to find the shortest route that visits each city (vertex) exactly once.

How many edges are in a complete graph?

In a complete graph with $ n $ vertices, there are exactly $ \frac{n(n-1)}{2} $ edges because each vertex is connected to all the others.

This formula comes from the fact that each vertex can connect to $ n-1 $ other vertices, but each edge is counted twice (once for each of its two vertices), so we divide by 2.

Practical Example

Let's consider a graph with 5 vertices: A, B, C, D, E.

In a complete graph:

A is connected to B, C, D, and E
B is connected to A, C, D, and E
C is connected to A, B, D, and E
D is connected to A, B, C, and E.

In total, there are 10 edges ($ \frac{5(5-1)}{2} = 10 $).

Here is a graphical representation.

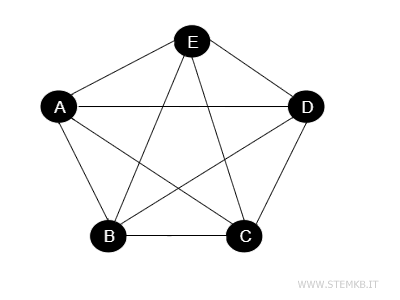
example of a complete graph with 5 vertices

The number of edges increases more than proportionally as the number of vertices grows.

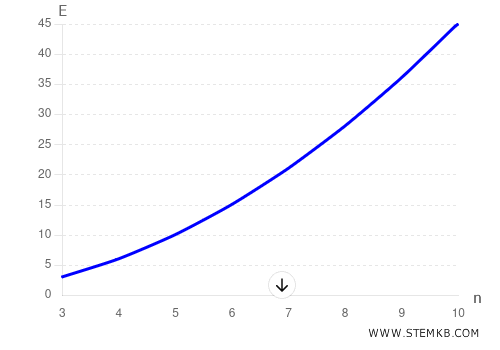
The formula $ \frac{n(n-1)}{2} $ shows that the number of edges grows quadratically with the number of vertices. For example:

For $ n = 2 $, we have $ E = \frac{2(2-1)}{2} = 1 $ edge.
For $ n = 3 $, we have $ E = \frac{3(3-1)}{2} = 3 $ edges.
For $ n = 4 $, we have $ E = \frac{4(4-1)}{2} = 6 $ edges.
For $ n = 5 $, we have $ E = \frac{5(5-1)}{2} = 10 $ edges.
For $ n = 6 $, we have $ E = \frac{6(6-1)}{2} = 15 $ edges.
For $ n = 7 $, we have $ E = \frac{7(7-1)}{2} = 21 $ edges.
For $ n = 8 $, we have $ E = \frac{8(8-1)}{2} = 28 $ edges.
For $ n = 9 $, we have $ E = \frac{9(9-1)}{2} = 36 $ edges.
For $ n = 10 $, we have $ E = \frac{10(10-1)}{2} = 45 $ edges.

As you can see, the number of edges increases rapidly as the number of vertices grows.

Here is a Cartesian diagram showing the number of edges as a function of the number of vertices $(n)$ from 3 to 10 in a complete graph.

the number of edges in a complete graph as the number of vertices varies

If you try to draw a complete graph with a large number of vertices, be prepared for a tangled mess of lines! If you don't believe it, try drawing a complete graph with 10 vertices and see the chaos.

In summary, a complete graph represents a network where everything is interconnected. It is the perfect example of total connectivity, both theoretically and practically.