Introduction to Graphs

Imagine a graph as a web of dots interconnected by lines. These dots are called "vertices" (or nodes), and the lines that connect them are referred to as "edges".

• Vertices (or nodes)
  Vertices are the individual points or nodes within this network, symbolizing the graph's objects or entities. Typically depicted as circles or dots, they're often labeled (e.g., "A", "B", "C", etc.).
  

  The total count of vertices is known as the order of the graph. For example, a graph with five vertices has an order of 5.

• Edges
  Edges are the links between vertices, similar to roads that connect cities. They symbolize the connections or relationships between vertex pairs. Generally, these links are called "edges" when directionless and "arcs" when directional.
  

  The total number of these links is referred to as the size of the graph. For instance, a graph with seven connecting lines has a size of 7.

A graph is denoted by G=(V,E), where G represents the graph itself, V is the set of vertices, and E embodies the collection of edges.

$$ G = (V,E) $$

The vertex set V encompasses all the labels assigned to the graph's vertices.

For example, the set of vertices for the graph mentioned earlier is as follows:

$$ V = \{ A,B,C,D,E \} $$

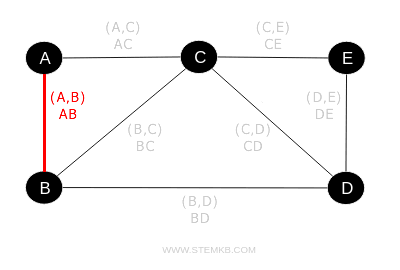
To represent an edge, one might write a pair (A,B) or simply AB, where "A" and "B" are the edge's endpoints.

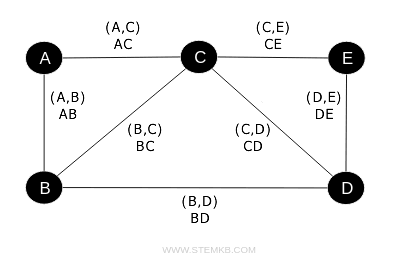
As an illustration, the edge collection for the previously discussed graph is:

$$ V = \{ AB, AC, BC, BD, CD, CE, DE \} $$

This collection comprises seven edges.

In a graph, each edge connects two vertices, also known as endpoints. These vertices may or may not be the same.

It's important to note that we use "collection" rather than "set" because a graph may have multiple lines connecting the same pair of vertices. Unlike a set, where each element is unique, a collection can include repeated elements, enabling the representation of several connections between the same vertex pairs. For a clearer understanding, consider a graph with multiple edges between vertices A and B, known as parallel edges.

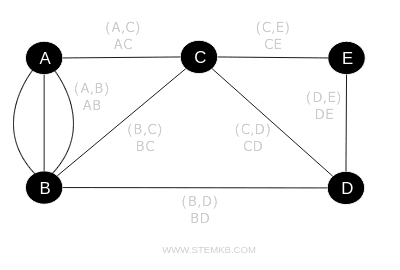
When two vertices are joined by an edge, they are described as being "incident" to that edge, which, in turn, is "incident" to the vertices.

For instance, the edge AB is incident to vertices A and B, and vice versa.

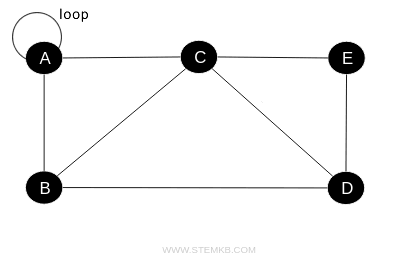
An edge that loops from a vertex back to itself is termed a "loop".

An example is a loop at vertex A in this graph.

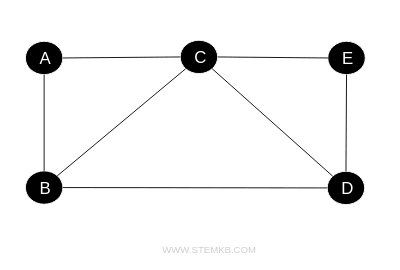
A simple graph lacks parallel edges and loops, offering a streamlined version of a graph with a single edge connecting any two vertices without any self-connecting edges.

Conversely, a pseudograph includes at least one loop, and a multigraph contains parallel edges without loops.

In closing this thorough introduction, we define a graph as complete when it features a direct connection between every pair of vertices within it.

Graph Applications: Graphs are instrumental in modeling relationships between objects, facilitating the depiction of intricate networks across various domains such as computer networks, electrical circuits, roadways, social networks, and much more.

Types of Graphs

Graphs are categorized based on distinct characteristics:

• Directed and Undirected Graphs
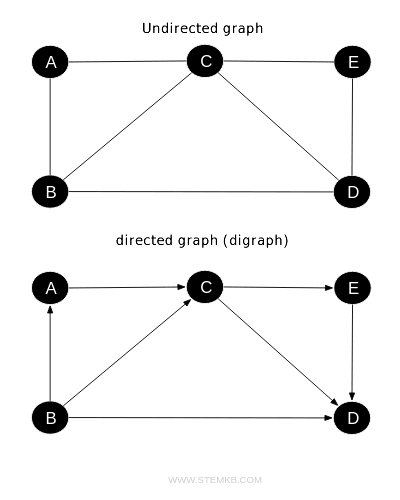
  Undirected graphs feature edges that lack specific directionality, merely indicating a connection between two vertices. Conversely, directed graphs (or digraphs) include edges with clear directional flow, denoting a directed relationship between the vertices they connect.
  

  

• Weighted and Unweighted Graphs
  Weighted graphs assign a numerical value or weight to each edge, which can represent various metrics such as cost or distance. In contrast, unweighted graphs treat all connections equally, without any associated weights.
  
• Cyclic and Acyclic Graphs
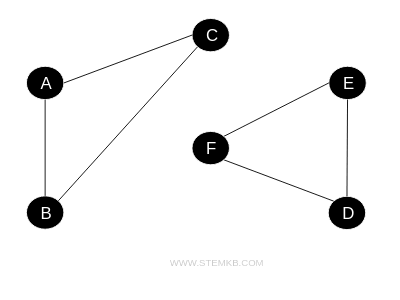
  A cyclic graph contains one or more closed loops or cycles, where a path can start and end at the same vertex. An acyclic graph, on the other hand, does not contain any cycles.
• Connected and Disconnected Graphs
  A graph is considered connected if there is a path between every pair of vertices. A disconnected graph has at least two vertices that cannot be reached from each other.
• Bipartite Graph
  Picture a scenario where you can organize the vertices into two distinct groups, ensuring that edges only form connections between vertices of separate groups, avoiding any intra-group connections. This configuration is identified as a "bipartite" graph. Furthermore, a bipartite graph reaches a state of completeness when each vertex in one group establishes a connection with every vertex in the opposing group.
  

These diverse characteristics make graphs versatile tools for a wide array of applications, from optimizing shortest paths to modeling complex networks and exploring game theory.

In both theoretical and practical computer science, essential tools and algorithms for working with graphs include depth-first search (DFS), breadth-first search (BFS), Dijkstra's algorithm for shortest paths, and Kruskal's algorithm for finding minimum spanning trees.

Directed and Undirected Graphs

Distinguishing between directed and undirected graphs is crucial, as it affects how edges within the graph facilitate connections between vertices.

Undirected Graphs

Edges in an undirected graph serve as two-way connections, depicted by simple lines without arrows, indicating mutual accessibility between vertices.

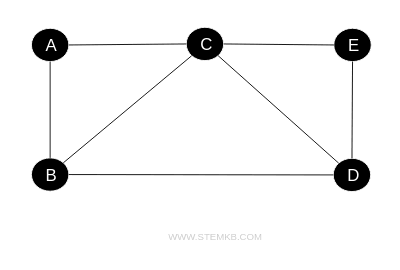
This bidirectional nature is ideal for modeling relationships where the direction of interaction is not significant, such as mutual friendships on social networks, bidirectional communication networks, or two-way traffic road systems.

Applications of undirected graphs include social network platforms like Facebook, where friendships are reciprocal, computer networks with two-way communication, and road maps with streets that accommodate traffic in both directions.

Directed Graphs (Digraphs)

Directed graphs, or digraphs, introduce a sense of direction to the connections between nodes, with arrows illustrating the path from one node to another.

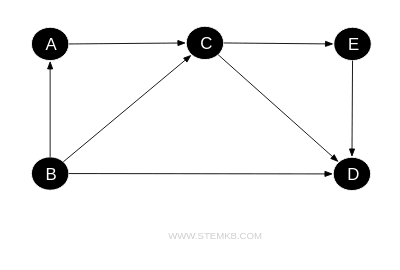
This directional attribute makes digraphs suitable for representing asymmetric relationships, such as following a user on social media without reciprocal following or road networks with one-way streets.

Directed graphs prove invaluable in depicting scenarios where relationships are unidirectional, illustrating the dynamics of social media interactions, transportation systems, and more, with precision and clarity.

Weighted Graphs

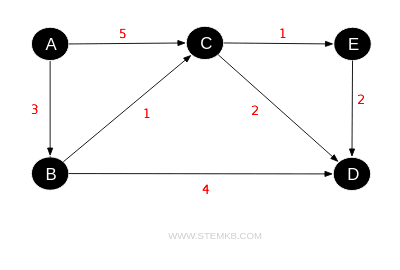
In a weighted graph, each edge is assigned a specific value, or weight, which can signify various metrics such as distances, costs, or time, offering a versatile tool for modeling and analyzing connections between pairs of nodes.

Take a road map as an example: cities are represented as nodes, with roads as edges between them. The weight of an edge could denote the distance between cities, the average time it takes to travel, or the cost of the journey. Consider finding the shortest path from node A to node D. While several routes exist, the most cost-effective is A→B→C→D, with a total cost of six (3+1+2=6).

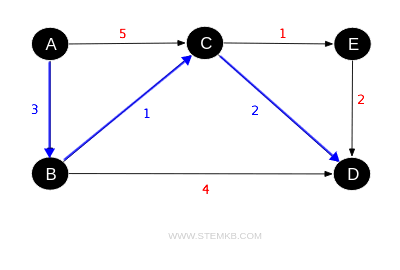
Other routes from node A to node D incur higher costs. For instance, traveling from A→C→D costs 7, A→C→E→D costs 8, and A→B→D costs 7.

Mathematically, a weighted graph is defined as a triple \(G = (V, E, w)\), where:

• \(V\) is the set of vertices or nodes.
• \(E\) is the set of edges, each representing a connection between a pair of nodes.
• \(w: E \rightarrow \mathbb{R}\) maps each edge to a weight, adding a layer of complexity and utility to the graph.

For instance, the vertex set V of the graph G above is

$$ V = \{ A, B, C, D, E \} $$

and its edge set E is

$$ E = \{ AB, AC, BC, BD, CD, CE, ED \} $$

with each edge's weight given as a pair in the set

$$ w = \{ (AB,3), (AC,5), (BC,1), (BD,4), (CD,2), (CE,1), (ED,2) \} $$

where the first element denotes the edge and the second its weight.

Key to the study of weighted graphs are algorithms such as Dijkstra’s for pinpointing the shortest path between two nodes, and Prim's or Kruskal's for identifying a minimum spanning tree, ensuring all nodes are interconnected at the lowest aggregate cost.