Incidence Matrix in Graph Theory

An incidence matrix is a fundamental concept in graph theory, structured to map the connections between vertices and edges in a graph. The rows of this matrix represent vertices, while the columns correspond to edges.

It serves as an alternative mathematical representation for graphs, applicable to both directed (digraphs) and undirected graphs.

Incidence Matrix in Undirected Graphs
Incidence Matrix in Directed Graphs

Incidence Matrix in Undirected Graphs

In an undirected graph, the incidence matrix is a rectangular $ n \times m $ matrix where $ n $ denotes the number of vertices and $ m $ the number of edges.

Each column of the matrix stands for an edge in the graph, with each row indicating a vertex. The elements of the matrix are populated as follows:

1 marks the presence of an endpoint of an edge at the vertex corresponding to the row
0 indicates the absence of an endpoint of an edge at the vertex corresponding to the row

This matrix contrasts with the adjacency matrix, which concentrates on direct vertex-to-vertex relationships, whereas the incidence matrix focuses on vertex-to-edge relationships.

Example

Consider a simple undirected graph with four vertices $ A, B, C, D $ and four edges $ e_1, e_2, e_3, e_4 $, where:

$ e_1 $ connects $ A $ and $ B $
$ e_2 $ links $ B $ and $ C $
$ e_3 $ joins $ C $ and $ D $
$ e_4 $ ties $ D $ and $ A $

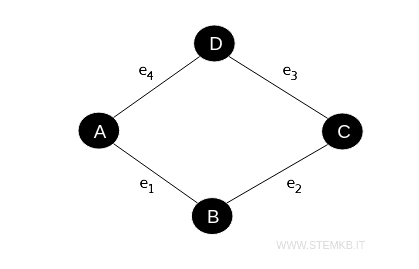
An example of an undirected graph with 4 vertices and 4 edges

The corresponding incidence matrix is displayed below:

$$
\begin{array}{c|cccc}
& e_1 & e_2 & e_3 & e_4 \\
\hline
A & 1 & 0 & 0 & 1 \\
B & 1 & 1 & 0 & 0 \\
C & 0 & 1 & 1 & 0 \\
D & 0 & 0 & 1 & 1 \\
\end{array}
$$

Incidence Matrix in Directed Graphs

For digraphs, the incidence matrix is adapted to reflect the directional nature of the edges.

In this setup, rows still represent vertices, but the columns now correspond to directed edges or arcs. The entries in the matrix are defined as:

-1 if the vertex is the source of the directed edge
1 if the vertex is the target of the directed edge
0 if the vertex is not involved with the edge

This arrangement provides a clear depiction of how vertices are interconnected through directed edges, making it especially useful for analyzing graph connectivity and pathfinding.

In the incidence matrix for a digraph, the sum of the values in each column will always be zero, indicating that each arc has a distinct source and target vertex.

Example

For instance, consider a digraph with vertices $ A, B, C, D $ and directed edges $ e_1, e_2, e_3, e_4 $ configured as follows:

$ e_1 $ proceeds from $ A $ to $ B $
$ e_2 $ extends from $ B $ to $ C $
$ e_3 $ moves from $ C $ to $ D $
$ e_4 $ leads from $ D $ back to $ A $

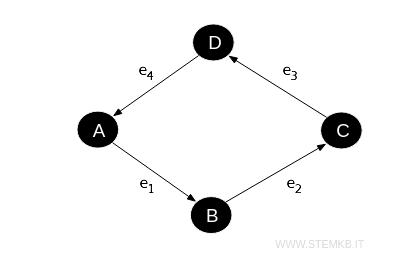
An example of a directed graph

The incidence matrix for this digraph is laid out below:

$$
\begin{array}{c|cccc}
& e_1 & e_2 & e_3 & e_4 \\
\hline
A & -1 & 0 & 0 & 1 \\
B & 1 & -1 & 0 & 0 \\
C & 0 & 1 & -1 & 0 \\
D & 0 & 0 & 1 & -1 \\
\end{array}
$$

It's worth noting that various representations may adopt different conventions to denote the directions of arcs, or the presence of loops in digraphs, depending on the specific context or software being used.

Overall, the incidence matrix proves invaluable for examining graph structures in terms of vertex and edge connections, aiding significantly in both theoretical studies and practical applications.