Adjacent Vertices in Graph Theory

Within the field of graph theory, adjacent vertices refer to a pair of vertices (or nodes) that are linked by a single edge (or arc).

This means if an edge connects two vertices, those vertices are considered adjacent.

Take, for example, a graph where vertices A and C are adjacent because they're connected by the edge AC.

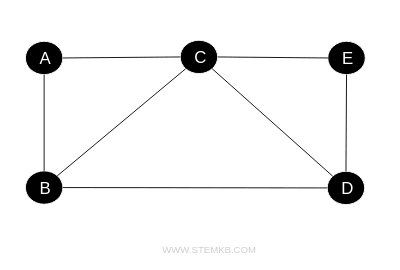
example of a simple graph

Similarly, vertices AB are adjacent due to the direct connection via edge AB. On the other hand, nodes A and D are not adjacent because there isn't a direct link between them.

The collection of vertices that are adjacent to a particular vertex $V$ in a graph forms what is known as the neighborhood of $V$.

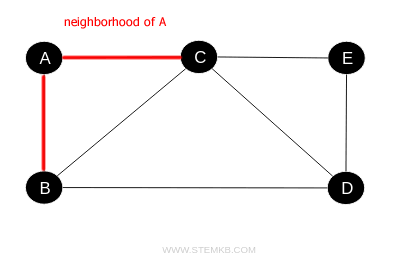
example of a vertex's neighborhood

The quantity of vertices adjacent to a vertex $ V $—in other words, the size of $ V $'s neighborhood—is termed the degree of the vertex $ V $.

Understanding the concept of neighborhoods is essential for analyzing the intricate web of relationships and connections among vertices in a graph.

It's important to note that adjacency doesn't require vertices to be close to each other in a physical sense; the critical factor is their direct connection via an edge or arc.

For instance, the neighbors of vertex A in this graph include nodes B and C, making A's degree 2. Vertex B's neighbors are A, C, and D, indicating a degree of 3 for B. Vertex C is directly connected to every other vertex, giving it a degree of 4, and so on.
example of a simple graph

Adjacent vertices are fundamental as they establish the graph's structure and dictate the dynamics of node interrelations.

For example, every vertex in a connected graph is adjacent to at least one other vertex.

This characteristic is pivotal to the definition of a connected graph, highlighting that isolated vertices, or those without any connecting edges to other vertices, contradict the principle of graph connectivity.

Adjacency in Directed Versus Undirected Graphs

Adjacency is a principle that applies equally to both directed and undirected (simple) graphs.

In a simple (undirected) graph, adjacency is bidirectional: if vertex $A$ is adjacent to $B$, then $B$ is inherently adjacent to $A$.
In a directed graph (digraph), adjacency takes into account the directionality of edges. This means if there's a directed edge from $A$ to $B$, $A$ is considered adjacent to $B$, but not necessarily the other way around unless there is also a directed edge from $B$ to $A$. For instance, in this digraph, A is adjacent to B but not vice versa.

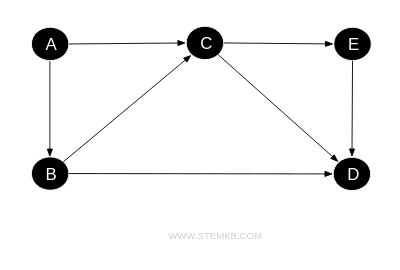
The distinction between adjacency in simple graphs and digraphs underscores the nuanced differences brought about by edge directionality in digraphs.

This nuance is particularly significant when calculating the degree of vertices in digraphs, as it necessitates consideration of both incoming and outgoing edges.