Disjoint Graphs

A set of disjoint graphs consists of two or more graphs that have no vertices or edges in common.

Simply put, graphs are disjoint if each one operates in complete isolation from the others, maintaining total independence.

This characteristic of disjoint graphs allows for each one to be analyzed or manipulated without reference to any other, which can significantly streamline data analysis and processing tasks.

Example

Take, for example, two graphs, G1 and G2, which are disjoint because they share no common vertices or edges.

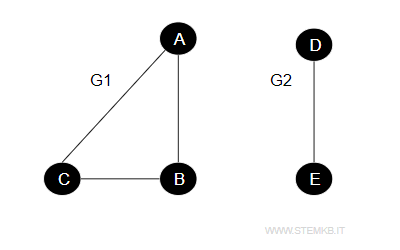
Each graph stands alone, independent from the other.

• Graph G1 is formed from vertices {A,B,C} and edges {AB, AC, BC}.
• Graph G2 comprises vertices {D,E} and the single edge {DE}.

Their disjoint nature ensures they remain entirely separate, with no points of intersection.

Merging these two graphs $ G1 \cup G2 $ results in a new graph including vertices A, B, C, D, E and edges AB, AC, BC, and DE. Yet, this amalgamated graph maintains its disjoint status as the original graphs retain their distinct separateness.

Understanding disjoint graphs is fundamental when delving into algorithms that handle partitioned groups of elements into distinct sets. It facilitates the quick determination of whether two elements are part of the same group.