Connected and Strongly Connected Digraphs

A digraph is considered connected if, when ignoring edge directions, there’s a path between every pair of nodes. It’s strongly connected if, following the direction of the edges, it’s possible to reach any node starting from any other node.

Let's explore this difference with some practical examples.

A digraph (or directed graph) is termed "connected" if there’s a path between any pair of vertices, provided you ignore the direction of the edges.

In other words, viewing the graph as undirected—disregarding edge directions—lets you reach any vertex from any other.

Here’s an example featuring a digraph with 5 nodes A, B, C, D, E and 5 edges (A,B), (B,C), (C,D), (D,A), (E,D).
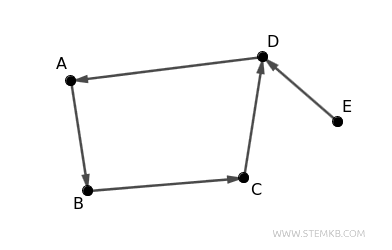
example of a connected digraph
This digraph is connected because, by removing the direction from each edge, you can reach every node from any other.
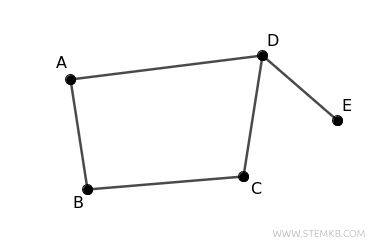
a graph

However, a "strongly connected" digraph requires more than just ignoring edge directions—you must be able to reach every vertex from any other vertex while respecting the edge directions.

This requirement is stricter, as it demands directed paths between each pair of vertices.

Here’s another example with a digraph of 5 nodes A, B, C, D, E and 5 edges (A,B), (B,C), (C,D), (D,A), (E,D). This graph is connected but not strongly connected, because, for instance, you cannot reach node E from node D.
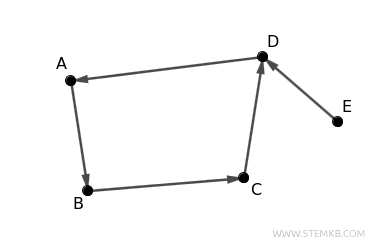
example of a connected digraph
In this scenario, edge direction matters. To make the digraph strongly connected, you would need to add at least one edge linking node \(E\) to another existing node. For example, adding an edge from \(C\) to \(E\) (i.e., \(C \to E\)) renders the digraph strongly connected, as there is now a directed path between every pair of nodes, making each node accessible from any other.
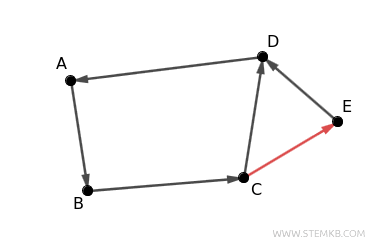
a graph

It follows that every strongly connected digraph is also connected, but not all connected digraphs are strongly connected.

This distinction is essential in practical applications like designing transportation or communication networks, where it’s crucial to know if nodes remain connected when you can only follow paths in a specific direction.