Edge Connectivity of a Graph

Edge connectivity of a graph refers to the minimum number of edges that must be removed to make a connected graph disconnected. This is denoted by $ λ(G) $.

In other words, it's the fewest number of edges you need to remove to ensure that at least one pair of vertices can no longer be connected by any path, thereby splitting the graph into two or more disconnected components.

Edge connectivity reflects how resilient a graph is to the removal of edges.

It indicates the number of edges that must be removed to disrupt the connectivity between the vertices of the graph.

Edge connectivity is crucial in many fields, such as communication networks, where it is important to ensure that the network remains connected even if some connections (edges) fail. A graph with higher edge connectivity is considered more robust than one with lower edge connectivity because it can tolerate the removal of more edges before becoming disconnected.

A graph is described as "k-edge-connected" if its edge connectivity is at least k, meaning that it takes a minimum of k edges to disconnect it, $ \lambda(G) \ge k $.

Example

Consider a graph consisting of a triangle (three vertices connected by three edges).

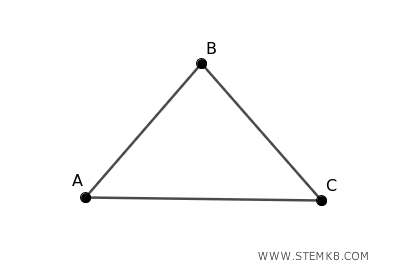
This is a connected graph because there is a path between every pair of vertices.

The edge connectivity $λ(G)$ of this graph is 2, because at least two edges must be removed to disconnect the graph, ensuring that at least one pair of vertices can no longer be connected by any path.

$$ λ(G) = 2 $$

For instance, you can disconnect the graph by removing edges (A,B) and (A,C) or edges (B,C) and (A,B).

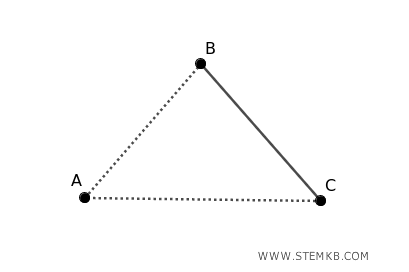
Thus, the graph is 2-edge-connected, meaning that at least two edges must be removed to disconnect it.

This implies that the graph is both 1-edge-connected and 2-edge-connected, as it takes the removal of at least two edges to make it disconnected. However, it is not 3-edge-connected.

Menger’s Theorem on Graph Connectivity

A graph \( G \) is k-edge-connected if and only if any two distinct vertex sets in \( G \) are linked by at least \( k \) edge-disjoint paths—paths that don’t share any edges.

This theorem, introduced by Austrian mathematician Karl Menger, connects a graph’s connectivity to the count of edge-disjoint paths between two sets of vertices.

Menger’s theorem provides an equivalent condition for k-edge-connectivity: a graph remains connected even when up to \( k-1 \) edges are removed.

To be k-edge-connected means that disconnecting two sets of vertices requires removing at least \( k \) edges.

Thus, if two distinct vertex sets are connected by at least \( k \) edge-disjoint paths, the graph exhibits a certain resistance to disconnection.

An example in practice

Consider the previous example of a graph with three vertices \( A \), \( B \), and \( C \) and three edges: \((A, B)\), \((B, C)\), and \((A, C)\).

Let’s see how Menger's theorem applies to k-edge-connectivity in this context. 

In this graph, any pair of vertices is connected by at least two edge-disjoint paths. For example:

• Between \( A \) and \( C \), two edge-disjoint paths exist:
  1. The direct path \((A, C)\),
  2. The indirect path \((A, B) \rightarrow (B, C)\).
• Between \( A \) and \( B \), there are also two edge-disjoint paths:
  1. The direct path \((A, B)\),
  2. The indirect path \((A, C) \rightarrow (C, B)\).
• Between \( B \) and \( C \), two edge-disjoint paths exist:
  1. The direct path \((B, C)\)
  2. The indirect path \((B, A) \rightarrow (A, C)\).

Since each pair of distinct vertices is connected by at least two edge-disjoint paths, the graph is 2-edge-connected.

In other words, according to Menger’s theorem, because each pair of vertices has two paths without shared edges, at least two edges must be removed to disconnect any vertex pair.

If we remove only one edge, all three vertices remain connected.

For instance, to disconnect vertices \( A \) and \( C \), both \((A, B)\) and \((B, C)\) or \((A, C)\) and another edge must be removed.

Thus, Menger's theorem holds here: this graph is 2-edge-connected, meaning each pair of distinct vertices is linked by at least two edge-disjoint paths.

This indicates the graph’s robustness: connectivity between vertices is maintained until at least two edges are removed. 

Menger's theorem offers a powerful way to characterize connectivity through disjoint paths.