Graph Paths

A path in a graph is a finite sequence of edges where each vertex is distinct, ensuring that each pair of consecutive edges in the sequence shares a common vertex.

In other words, a path does not pass through the same vertex more than once, except potentially for the starting and ending vertices in the case of closed paths (or cycles).

Each vertex in the graph appears at most once along the path.

A path with vertices $ v_1, v_2, \ldots, v_n $ can be represented as a sequence of vertices $ (v_1, v_2, \ldots, v_n) $ or as a sequence of edges $ (e_1, e_2, \ldots, e_{n-1}) $, where each edge $ e_i $ connects vertices $ v_i $ and $ v_{i+1} $.

Example

Consider a graph with 5 vertices (A, B, C, D, E) and 7 edges (AB, AC, BC, BD, CE, CD, DE).

simple graph example

To define a path starting from vertex A and ending at vertex D, we could choose the following sequence of vertices: $ A \rightarrow B \rightarrow C \rightarrow D $

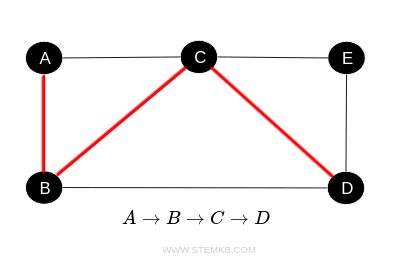
path example

This path is represented by the sequence of vertices A, B, C, D and the sequence of edges AB, BC, CD.

Each vertex is visited only once, making it a simple path. In this case, the path is not closed because it starts and ends at different vertices.

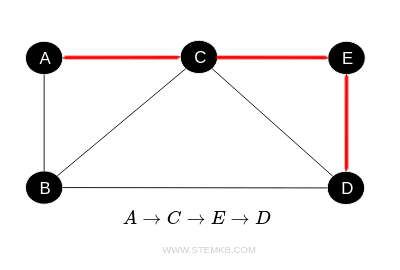
Another path connecting vertices A and D is: $ A \rightarrow C \rightarrow E \rightarrow D $

another path

To create a closed path that starts and ends at the same vertex, we could have: $ A \rightarrow B \rightarrow D \rightarrow C \rightarrow A $

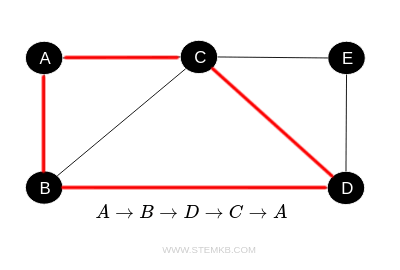
an example of a closed path

This still qualifies as a path because each vertex is visited only once, except for vertex A, which serves as both the starting and ending point.