Adjacency Matrix of a Graph
An adjacency matrix is a square matrix used to determine adjacency between vertices in a graph, meaning it shows which vertices are directly connected by an edge.
This tool is essential for representing graphs in a mathematical format.
Building an Adjacency Matrix for a Graph
A graph is composed of vertices (or nodes) and edges (or arcs) that link these vertices. Think of vertices as points and edges as the lines that connect these points.
An adjacency matrix for a graph with \( n \) vertices is an \( n \times n \) square matrix, consisting of $ n $ rows and $ n $ columns.
Each matrix row and column is associated with a vertex in the graph.
Matrix elements are either 0 or 1:
- 1 indicates the presence of a direct edge between the corresponding vertices.
- 0 indicates the absence of a direct edge between the corresponding vertices.
In certain instances, other values may be used if the edges are weighted or if multiple edges exist between the same pair of vertices.
Example
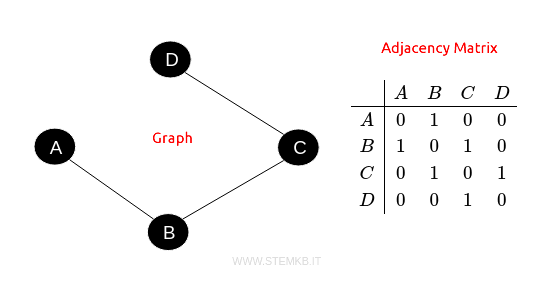
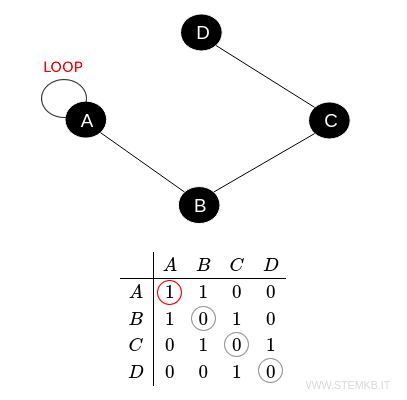
Consider a graph with four vertices: \( A, B, C, \) and \( D \).
Let's say there are edges between \( A \) and \( B \), \( B \) and \( C \), and \( C \) and \( D \).
The adjacency matrix for this graph, with vertices ordered as \( A, B, C, D \), will be:
$$ \begin{array}{c|cccc} & A & B & C & D \\ \hline A & 0 & 1 & 0 & 0 \\ B & 1 & 0 & 1 & 0 \\ C & 0 & 1 & 0 & 1 \\ D & 0 & 0 & 1 & 0 \\ \end{array} $$
Cells representing unconnected vertices have a value of 0, while those representing connected vertices display a value of 1.
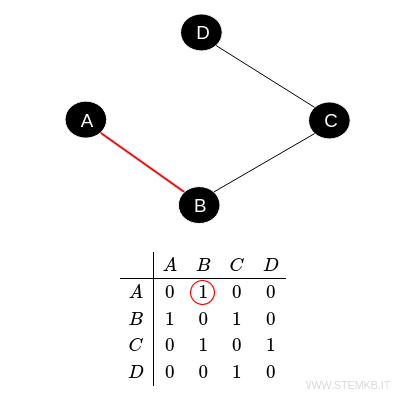
For instance, the cell at row \( A \) and column \( B \) is valued at 1, indicating an edge connecting \( A \) to \( B \).
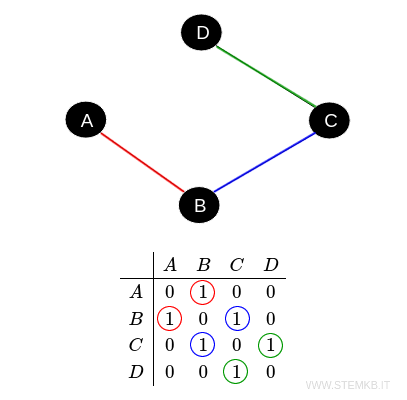
For undirected graphs, the adjacency matrix is symmetric, meaning if vertex \( A \) is connected to \( B \), then \( B \) is connected back to \( A \).
If the graph features loops, i.e., edges that start and end at the same vertex, the main diagonal of the matrix will show non-zero values.
This representation allows for the quick visualization and analysis of relationships between vertices in a graph, simplifying the implementation of graph algorithms on computers.
Adjacency Matrix in Directed Graphs (Digraphs)
In digraphs, where edges are directional and flow from one vertex to another, the adjacency matrix functions a bit differently.
What is a digraph? A digraph is a type of graph with directed edges.
The adjacency matrix for a digraph is still a square \( n \times n \) matrix when the graph has \( n \) vertices, but the rows and columns represent the source and destination vertices, respectively.
- 1 in position \( (i, j) \) means there is an edge from vertex \( i \) to vertex \( j \).
- 0 in position \( (i, j) \) means there is no direct edge from \( i \) to \( j \).
Example
For a digraph with four vertices \( A, B, C, \) and \( D \), and directed edges from \( A \) to \( B \), from \( B \) to \( C \), and from \( C \) to \( D \):
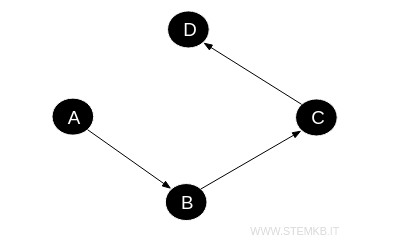
The adjacency matrix for this digraph will be:
$$ \begin{array}{c|cccc} & A & B & C & D \\ \hline A & 0 & 1 & 0 & 0 \\ B & 0 & 0 & 1 & 0 \\ C & 0 & 0 & 0 & 1 \\ D & 0 & 0 & 0 & 0 \\ \end{array} $$
Here, the "1" value illustrates the direction of the edge, such as from \( A \) to \( B \), but not in the reverse direction.
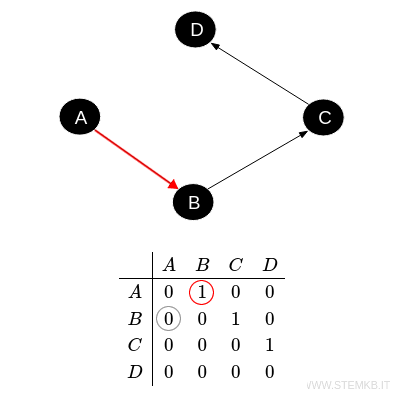
As evident, the adjacency matrix of a digraph is not symmetrical, unless the graph features bi-directional edges between the same nodes.
The adjacency matrix in a digraph can also be used to check for paths from one vertex to another and analyze the graph's structure in terms of connectivity and reachability. This setup enables the execution of specific algorithms for digraphs, such as finding the shortest paths, computing strongly connected components, and other network analysis tasks that require edge directionality.

