Cutset of a Connected Graph

A cutset (or cut) of a connected graph is a minimal disconnecting set.

A disconnecting set is a set of edges in a connected graph whose removal makes the graph disconnected.

The cutset is the smallest disconnecting set of the graph, meaning no proper subset of the cutset can serve as a disconnecting set.

In other words, removing even one edge less than the entire cutset would leave the graph connected.

This implies that every cutset is a disconnecting set, but not all disconnecting sets are cutsets.

The removal of all edges in a cutset must divide the graph into two or more disconnected components.

This concept is fundamental in graph theory and closely related to the connectivity of a graph.

Example

Consider a graph with 6 vertices and 7 edges.

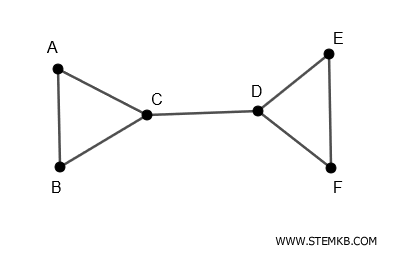
Suppose we want to find a cutset that disconnects the graph when removed.

If we remove the edges \((A-B)\) and \((B-C)\), the graph breaks into two components.

Therefore, the set $ \{ (A-B), (B-C)  \} $ is a disconnecting set of the graph.

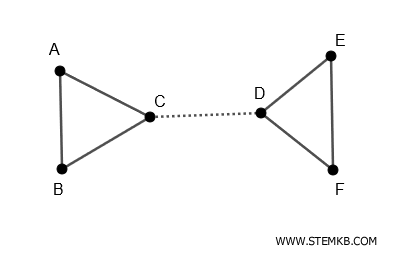
However, removing just the edge \( (C-D) \) also disconnects the graph into two parts.

Thus, the set $ \{  (C-D) \} $ is another disconnecting set of the graph.

Since there is no smaller disconnecting set than $\{ (C-D) \}$, we can conclude that it is also a cutset of the graph.

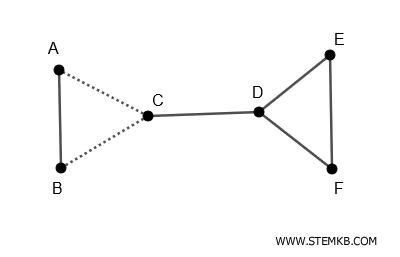
Conversely, the set $\{(A-B), (B-C)\}$ is a disconnecting set but not a cutset.

In general, when a cutset consists of a single edge, it is referred to as a bridge.

In summary, a cutset is a set of edges whose minimal removal is sufficient to disconnect a connected graph.

It is an essential tool for analyzing the connectivity and robustness of networks.