Multiple Edges in Graph Theory

Within graph theory, multiple edges refer to the phenomenon where two or more parallel edges (links or arcs) connect the same pair of vertices, intersecting nowhere.

Imagine them as diverse pathways from point A to B, offering distinct journeys that converge at identical endpoints.

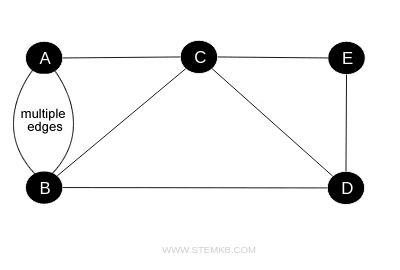
The existence of multiple edges adds a layer of complexity to graph analysis.

For a tangible illustration, envision a castle accessible through several trails from a single village. These trails embody the multiple edges in the graph, each providing a unique trek—be it crossing a quaint bridge or meandering through lush trees—yet both originating from the village and culminating at the castle.

There are principally two kinds of multiple edges:

• Arrows
  In directed graphs, multiple edges can manifest as arrows, bearing specific directions.
  
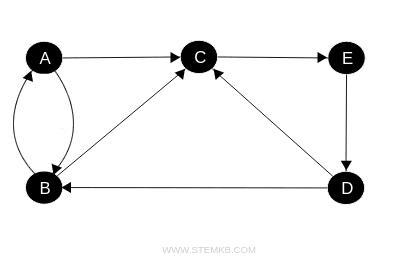
• Edges
  In undirected graphs, multiple edges surface as edges, devoid of any directional bias.
  

  

Far from being mere redundancies, these parallel paths represent different routing choices with their own sets of implications, such as travel length, challenge level, or the diversity of experiences they offer.

In graph theoretical terms, multiple edges shed light on more than just the straightforward connectivity between vertices; they reveal the nature and quality of the relationships binding these points.

Consider, for instance, the introduction of weights to edges, indicating distances. It becomes immediately evident that one path between vertices A and B is shorter than the other. Thus, if minimizing distance is the goal, opting for the 3 km path over the 5 km route is advisable.

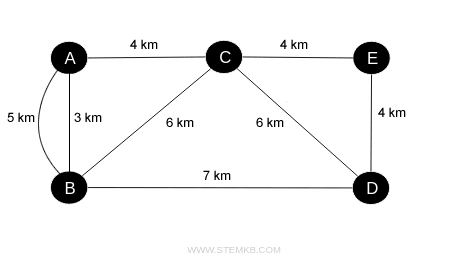
This addition of weights to multiple edges introduces a new dimension of complexity and significance to the graph's internal route calculations. In scenarios where weights represent distance, cost, time, or any quantifiable metric, the presence of multiple connections between the same pair of nodes, each bearing different weights, can significantly sway the choice of the optimal path.

The utility of multiple edges in graphs is vividly showcased in areas like transportation networks and electrical circuits.

• In transportation networks, the presence of multiple roads linking the same destinations is vital for designing efficient and resilient systems. For example, a network of roads connecting two major cities. Here, having multiple routes not only mitigates congestion risks but also offers alternatives in case of roadblocks or emergencies, thus ensuring greater reliability. Additionally, different routes can be optimized for specific purposes: some for heavy transport, others for faster travel, or to minimize environmental impact.
• For electrical circuits, parallel paths are essential in defining circuit characteristics, such as total resistance. Consider two resistors in parallel; this configuration not only provides an alternative current flow but also lowers the overall circuit resistance compared to each resistor individually. This principle allows for current distribution control and circuit performance optimization, crucial in power supply systems to maintain uniform load distribution.

The concept of parallel paths is not merely a theoretical curiosity but a practical attribute with tangible benefits across various applications.

By offering alternative routes between two nodes, multiple edges significantly enhance a graph's connectivity.

This feature proves invaluable in sectors where network resilience and robustness are paramount, like in communication networks, water distribution systems, or transport infrastructure.

Should a route become infeasible due to a fault or disruption, the availability of alternative paths ensures uninterrupted node connectivity, softening the blow of potential service failures. Moreover , such redundancy can be strategically leveraged to optimize flow within the graph, facilitating more efficient load distribution and minimizing bottleneck risks.

Ultimately, the flexibility to choose among various paths lends greater adaptability in addressing fluctuating needs and managing unexpected situations, enhancing the application of graph theory to real-world challenges.