Degree of a Vertex in Graph Theory

In the world of graph theory, the degree of a vertex \(V\) indicates how many vertices are directly linked to it, known as adjacent vertices.

Determining a vertex's degree depends on whether the graph is undirected (simple) or directed.

Vertex Degrees in Simple Graphs

In an simple graph, the degree of a vertex precisely matches the number of edges connected to it.

Take vertex A as an example: its degree is 2 because it shares connections with two other vertices (B and C). On the other hand, vertex B has a degree of 3, connecting it with three other vertices (A, C, D), and so on.

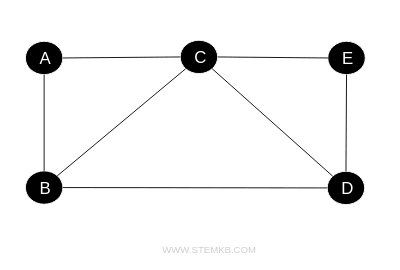
In this type of graph, a vertex with a degree of 0 stands alone, not connected to any other vertex. Meanwhile, a vertex with a degree of 1 connects to just one other vertex, and the pattern continues.

Vertex Degrees in Directed Graphs

In directed graphs (or digraphs), the process to calculate a vertex's degree is slightly more intricate. It's essential to differentiate between incoming and outgoing edges for each vertex.

Therefore, we recognize two distinct types of degrees for each vertex:

• In-degree
  A vertex's in-degree \(V\) is the total of directed edges heading towards \(V\), essentially how many vertices can lead to \(V\) by following the directional flow of the edges. It reflects the number of incoming connections or "dependencies" a vertex has.
• Out-degree
  Conversely, a vertex's out-degree \(V\) tallies the edges departing from \(V\), indicating the vertex's reach towards others or how often \(V\) acts as the origin to explore other nodes.

For instance, look at the following directed graph. Vertex A boasts an in-degree of 0 and an out-degree of 2, indicating no edges enter A, but two edges (AC and AB) extend from A to other vertices.

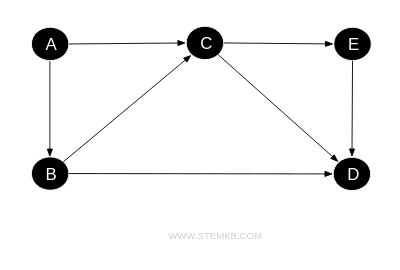
In essence, the sum of the in-degrees across all vertices in a digraph matches the sum of the out-degrees, with both totals equating to the overall number of edges within the digraph.

This phenomenon underscores the balance between incoming and outgoing connections, illustrating the fundamentally symmetrical nature of relationships in a directed graph.