Connected Graph

A connected graph is a graph where a path exists between every pair of vertices.

Simply put, you can travel from any vertex to any other through a series of edges.

Such graphs feature no isolated vertices or clusters, ensuring all vertices are interconnected.

Connectivity is a critical attribute for many practical applications, including the design of telecommunications networks, urban road planning, and electrical circuit theory, where accessibility of each component is essential.

Connectivity applies to both undirected graphs (simple graphs) and directed graphs (digraphs).

Connectivity in Simple Graphs

An undirected graph is connected if there is a path linking each vertex pair \( u \) and \( v \).

Connectivity in Digraphs

In directed graphs, connectivity means that for each vertex pair \( u \) and \( v \), paths exist from \( u \) to \( v \) and vice versa.

Example

Consider a connected graph with five vertices, numbered 1 through 5.

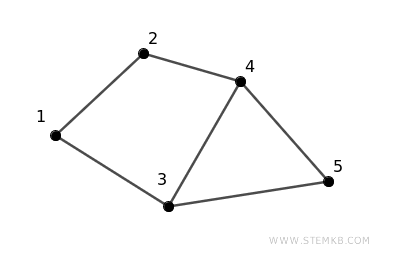
The edges are configured as follows:

• Vertex 1 connects to vertices 2 and 3.
• Vertex 2 is linked to vertex 4.
• Vertex 3 links to vertices 4 and 5.
• Vertex 4 links to vertex 5.

This setup ensures a connected structure, enabling travel from any vertex to another via connected edges.

For instance, a route from vertex 1 to vertex 5 might be via vertices 3 and 5: 1 -> 3 -> 5.

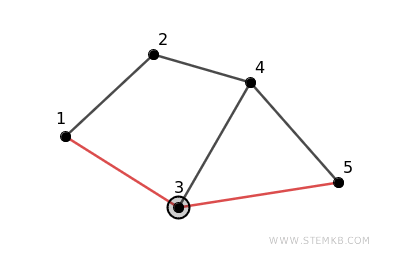
This structural connectivity guarantees no vertex is left isolated, with every vertex pair being either directly or indirectly connected through a network of vertices and edges.

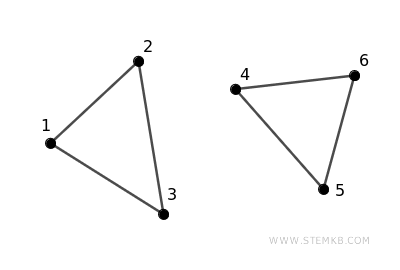
Example of an Unconnected Graph: This graph lacks connectivity as not all vertices are linked, either directly or indirectly. For example, there's no direct path from vertex 2 to vertex 4, nor from vertex 1 to vertex 6, etc.

Example of a Connected Digraph

Here's an example using a strongly connected digraph with five vertices:

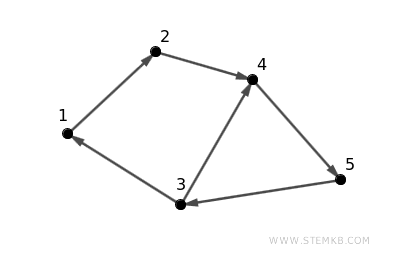
The connections are as follows:

• An arc from vertex 1 to vertex 2.
• An arc from vertex 2 to vertex 4.
• Arcs from vertex 3 to vertices 1 and 4.
• An arc from vertex 4 to vertex 5.
• An arc from vertex 5 back to vertex 3.

This digraph is connected because each vertex is reachable from any other through directed paths.

For example, the path 1→2→4→5 connects vertex 1 to vertex 5. Conversely, the path 5→3→1 connects vertex 5 back to vertex 1.

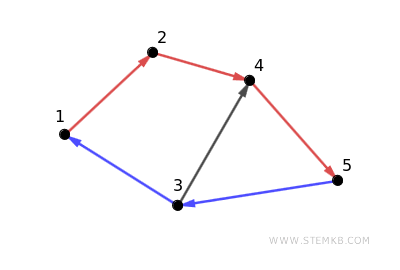
This digraph also completes a cycle that includes every vertex, demonstrating strong connectivity as it allows a return to the starting point following a directed sequence of edges.

The cycle 1→2→4→5→3→1 passes through every vertex, starting and ending at vertex 1.

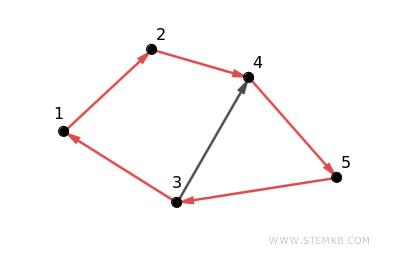
This example highlights the digraph as strongly connected, meeting the condition that for every vertex pair \( u \) and \( v \), directed paths run from \( u \) to \( v \) and back.

Conversely, a digraph is weakly connected if, disregarding edge directions, a path connects every vertex pair. If transforming all directed edges into bidirectional ones results in a connected structure, the digraph is then considered weakly connected.

For instance, this digraph isn't strongly connected because it's not possible to move from vertex 3 to vertex 4 directly.

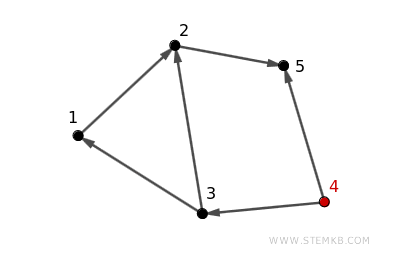
However, if considering all edges as bidirectional, a path exists connecting every vertex to any other, classifying the digraph as weakly connected.