Vertex Separating Set
A vertex separating set is a set of nodes (vertices) in a graph that, when removed, disconnects the graph.
In other words, by removing these vertices along with their associated edges, the graph is split into two or more subgraphs that are no longer connected.
This set is also known as a "vertex separator" or simply a "separating set."
A special concept within this context is the cut-vertex. This is a specific vertex that, if removed, disconnects the graph. It represents the simplest example of a separating set, consisting of a single vertex.
The connectivity of a graph, denoted as \( \kappa(G) \), is the minimum number of vertices that must be removed to disconnect the graph. Thus, the smallest separating set defines the graph's connectivity.
Example
Consider a connected graph with three vertices \( A \), \( B \), and \( C \), where \( A \) is connected to \( B \) and \( B \) is connected to \( C \).
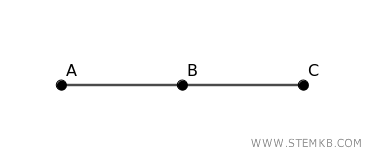
If vertex \( B \) is removed, the graph becomes disconnected, leaving \( A \) and \( C \) unconnected. In this scenario, \( B \) is a cut-vertex.
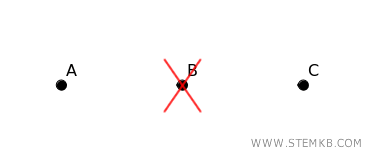
This graph has a connectivity of \( \kappa(G) = 1 \), indicating that it is 1-connected, since removing just one vertex is enough to disconnect it.
Example 2
Now, consider a connected graph with four vertices \( A \), \( B \), \( C \), and \( D \), with edges \( (A, B) \), \( (B, C) \), \( (C, D) \), and \( (D, A) \) forming a quadrilateral.
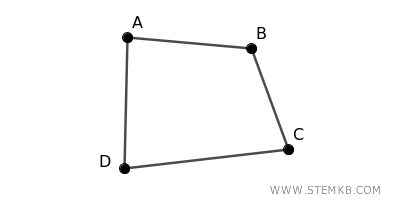
In this case, removing a single vertex is not sufficient to disconnect the graph, as the remaining three vertices are still interconnected.
For instance, if vertex \( A \) is removed, the connections between \( B \), \( C \), and \( D \) remain intact through edges \( (B, C) \) and \( (C, D) \).
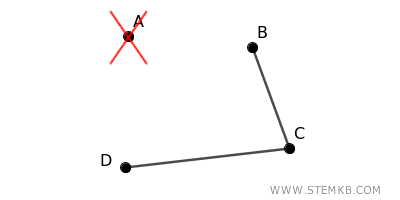
To fully separate this graph into disconnected parts, at least two vertices, such as \( A \) and \( C \) or \( B \) and \( D \), must be removed.
Therefore, this graph is 2-connected, with a connectivity of \( \kappa(G) = 2 \), since at least two vertices must be removed to disconnect it.
Menger's Theorem
An important theoretical result associated with separating sets is Menger's Theorem. This theorem states:
The connectivity of a graph (i.e., the minimum number of vertices that need to be removed to disconnect the graph) is equal to the maximum number of vertex-disjoint paths between any two vertices in the graph.
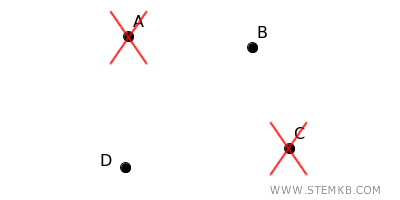
For example, consider two vertices \( A \) and \( B \) in a graph.

There are two distinct paths between \( A \) and \( B \) that do not share any vertices (except for \( A \) and \( B \)):
- $ A \rightarrow B $
- $ A \rightarrow D \rightarrow C \rightarrow B $
Therefore, the connectivity of the graph is at least 2.
Applications of Separating Sets
Vertex separating sets are crucial tools in graph theory, providing insights into the robustness and vulnerability of networks.
By analyzing how a graph can be disconnected through the removal of specific vertices, it is possible to make predictions about how to maintain network connectivity or identify critical points that need to be reinforced.
Separating sets are used to pinpoint the critical points in a network whose removal would disrupt the system.
Example. They are particularly useful in designing communication networks, where vertices might represent servers, and edges could be the connections between them. In network security or power grid analysis, separating sets help identify key components that must be protected to prevent system-wide collapse in the event of attacks or failures.

