Disconnecting Set in a Graph

A disconnecting set in a connected graph \( G \) is a set of edges whose removal increases the number of components of the graph, effectively making the graph disconnected.

In other words, a disconnecting set is a group of edges that, when removed, cause the connected graph to split into separate parts.

It's a key concept in the study of graph connectivity.

Identifying disconnecting sets is crucial in various applications. For instance, in a telecommunications or transportation network, it helps pinpoint critical or weak points and, consequently, potential vulnerabilities.

Example

Consider a connected graph \( G \) consisting of five vertices (A, B, C, D, E) and seven edges (A-B), (A-C), (A-D), (B-C), (C-D), (C-E), (D-E).

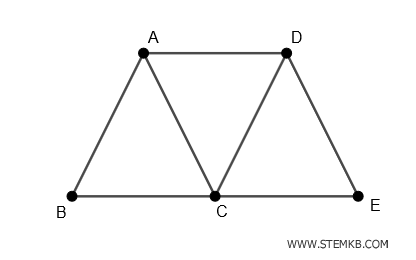
This graph is connected because there is a path between any pair of vertices.

Now, let's identify a disconnecting set consisting of the following edges:

$$ \{(A-B), (B-C) \} $$

If we remove these edges, we get two separate components:

• The first component consists of only vertex B
• The second component consists of vertices A, C, D, E

Therefore, by removing edges (A-B) and (B-C), the initially connected graph becomes disconnected.

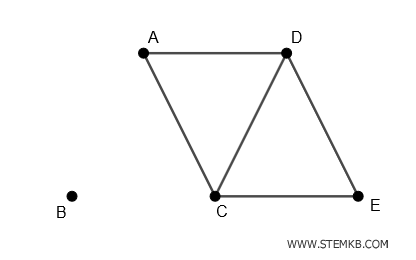
If the graph's vertices represented cities and the edges represented railway lines, this would mean that city B would be isolated in the event of simultaneous failures on lines (A-B) and (B-C). This example illustrates the practical importance of disconnecting sets.

A graph can also have more than one disconnecting set.

For example, in graph G another disconnecting set is the set of edges:

$$ \{(A-D), (D-C), (C-E) \} $$

Again, if we remove these edges, we get a disconnected graph consisting of two components:

The first component consists of vertices A, B, C while the second consists of vertices D, E.

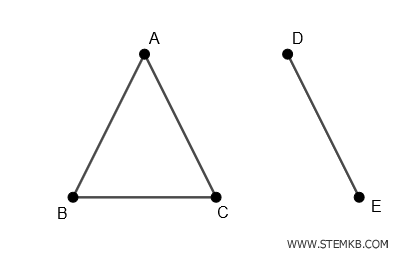
In summary, a graph can have many disconnecting sets.

The disconnecting set that removes the fewest edges in a graph is called a cutset.