Orientable Graph

An orientable graph is a graph in which you can assign a direction to each edge so that the resulting directed graph (digraph) becomes strongly connected.

A strongly connected graph allows you to reach any vertex from any other vertex by following the directions of the edges.

This strong connectivity ensures that, once oriented, there's a direct path between any two vertices.

An Example

Imagine a connected graph with 5 vertices labeled A, B, C, D, and E, along with edges that connect some pairs of these vertices.

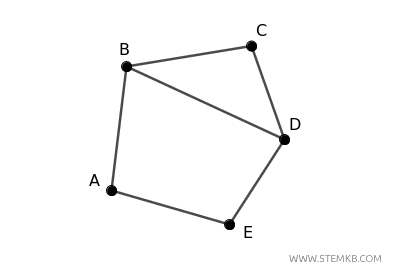
This graph is orientable because you can assign a direction to each edge to create a strongly connected directed graph.

For instance, suppose the edges are directed as follows:

• From \( A \) to \( B \) (arrow \( A \rightarrow B \))
• From \( B \) to \( C \) (arrow \( B \rightarrow C \))
• From \( C \) to \( D \) (arrow \( C \rightarrow D \))
• From \( D \) to \( E \) (arrow \( D \rightarrow E \))
• From \( E \) to \( A \) (arrow \( E \rightarrow A \))
• From \( B \) to \( D \) (arrow \( B \rightarrow D \))

The result is a strongly connected digraph, as you can reach any vertex from any starting point by following the directed edges.

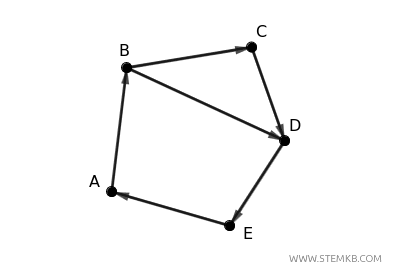
For example, starting from \( A \), you can reach \( C \) via \( B \) or reach \( E \) by moving through other nodes.

Therefore, the initial graph qualifies as an orientable graph.

Robbins' Theorem

According to Robbins' Theorem, a connected graph is orientable if and only if each edge is part of at least one cycle.

This requirement is both necessary and sufficient: each edge must be included in a cycle for the graph to be oriented in a way that it becomes strongly connected.

This means there should be no “dangling” or isolated edges in terms of cyclical connectivity; every edge must be part of a closed path (cycle).

Example

The 5-vertex graph from the previous example is orientable since each edge belongs to at least one cycle.

For instance, the cycle \( A \)-\( B \)-\( C \)-\( D \)-\( E \)-\( A \) includes all main edges, linking the vertices in a circular structure.

Alternatively, you could direct the edges differently to form two distinct cycles, A-B-D-E-A and B-D-C-B.

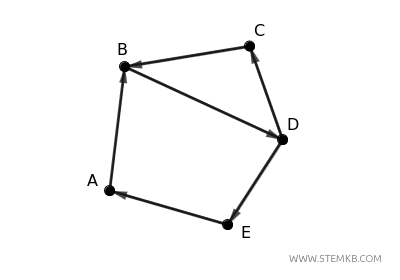
Again, all edges in the digraph participate in a cycle.

So, there are two clear reasons why the graph is orientable.

Proof of the Theorem

Here’s a look at how this theorem can be proven:

1. Necessary Condition: if an edge isn't part of any cycle, that edge would act as a “bottleneck” within the graph. This isolated edge would potentially separate vertices so that, once oriented, the graph could never become strongly connected.
2. Sufficient Condition: starting with any cycle in the graph, you can orient its edges in a circular fashion. For each new edge not yet part of an oriented cycle, consider another cycle that includes this edge and orient it to match the directions of edges already shared with other cycles. By repeating this process, all edges will eventually be directed while preserving the graph's connectivity.

The presence of cycles not only makes the graph easier to navigate but also enables its transformation into a fully connected, robustly directed structure.

This orientability is essential in applications like communication networks and transportation systems, where every node (or point) must be reachable from any other node without exception.