Graph Isomorphism

An isomorphism between two graphs \( G \) and \( H \) is a bijection between the vertices of \( G \) and \( H \) that preserves vertex connections. $$ G \cong H $$

In other words, two isomorphic graphs are essentially the same from a graph theory perspective, even if they appear different at first glance.

An isomorphism between two graphs allows you to "map" the vertices of one graph to the vertices of the other in such a way that the structures of both graphs are identical.

Formally, an isomorphism between two graphs \( G = (V_G, E_G) \) and \( H = (V_H, E_H) \) is a bijective function

$$ f: V_G \to V_H $$

such that for every \( u, v \in V_G \):

$$ \{u, v\} \in E_G \iff \{f(u), f(v)\} \in E_H $$

This means there is an edge between two vertices \( u \) and \( v \) in \( G \) if and only if there is an edge between the vertices \( f(u) \) and \( f(v) \) in \( H \).

Isomorphisms are important because they allow us to recognize when two graphs are "essentially the same." Two graphs belong to the same isomorphism class if there is an isomorphism between them. Thus, an isomorphism class is a group of graphs that are all isomorphic to each other. 

Example

Let's consider two simple graphs \( G \) and \( H \):

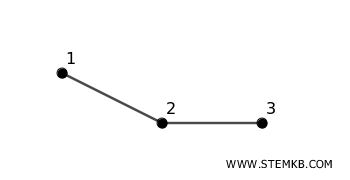
Graph \( G \)

Graph G has three vertices \( V_G = \{1, 2, 3\} \) and two edges \( E_G = \{\{1, 2\}, \{2, 3\}\} \)

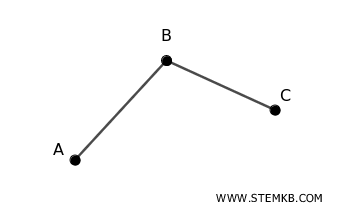
Graph \( H \)

Graph H has three vertices: \( V_H = \{A, B, C\} \) and two edges: \( E_H = \{\{A, B\}, \{B, C\}\} \)

A possible isomorphism \( f \) between \( G \) and \( H \) can be defined as follows:

$$ f(1) = A $$

$$ f(2) = B $$

$$ f(3) = C $$

Let's verify that \( f \) is an isomorphism:

\( \{1, 2\} \in E_G \rightarrow \{f(1), f(2)\} = \{A, B\} \in E_H \)

\( \{2, 3\} \in E_G \rightarrow \{f(2), f(3)\} = \{B, C\} \in E_H \)

Therefore, the function \( f \) preserves the vertex connections, making \( f \) an isomorphism between \( G \) and \( H \).

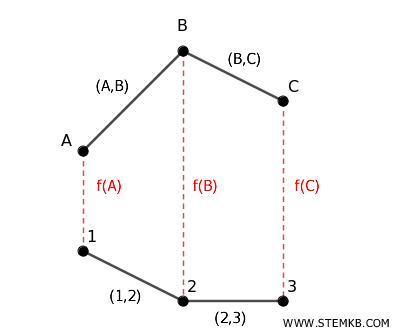
In conclusion, graphs G and H are isomorphic, so they belong to the same isomorphism class.

How to Check if Two Graphs Are Isomorphic

One method to check if two graphs are isomorphic is to relabel the vertices and compare their adjacency matrices.

Here's the procedure to verify isomorphism:

1. Construct adjacency matrices
   Build the adjacency matrices \( A_G \) and \( A_H \) for graphs \( G \) and \( H \).
2. Relabel the vertices
   Consider all possible permutations of the vertices of one of the graphs, for instance, \( G \).
3. Permute the matrices
   For each permutation, relabel the vertices of \( G \) and construct the corresponding adjacency matrix.
4. Compare the matrices
   Compare the relabeled adjacency matrix of \( G \) with the adjacency matrix of \( H \). If you find a permutation for which the matrices are identical, the graphs are isomorphic.

Let's look at a practical example

Consider two graphs \( G \) and \( H \):

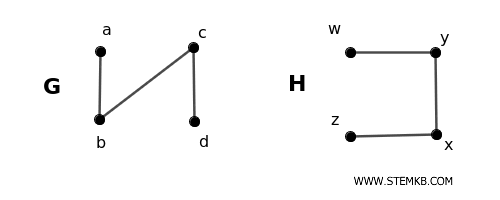
Graph G has four vertices \( V_G = \{a, b, c, d\} \) and three edges \( E_G = \{\{a, b\}, \{b, c\}, \{c, d\}\} \)

Graph H has four vertices \( V_H = \{w, x, y, z\} \) and three edges \( E_H = \{\{w, x\}, \{x, y\}, \{y, z\}\} \)

The adjacency matrices for \( G \) and \( H \) are respectively:

\[ A_G =
\begin{array}{c|cccc}
 & a & b & c & d \\
\hline
a & 0 & 1 & 0 & 0 \\
b & 1 & 0 & 1 & 0 \\
c & 0 & 1 & 0 & 1 \\
d & 0 & 0 & 1 & 0 \\
\end{array}
\]

\[ A_H =
\begin{array}{c|cccc}
 & w & y & x & y \\
\hline
w & 0 & 0 & 0 & 1 \\
y & 0 & 0 & 1 & 1 \\
x & 0 & 1 & 0 & 0 \\
y & 1 & 1 & 0 & 0 \\
\end{array}
\]

Now let's try some permutations of the rows and columns on matrix \( A_G \) to make it match matrix \( A_H \).

For example, move the second row/column to the third row/column ($ b \leftrightarrow c $).

\[ A_G =\begin{array}{c|cccc}
 & a & c & b & d \\
\hline
a & 0 & 0 & 1 & 0 \\
c & 0 & 0 & 1 & 1 \\
b & 1 & 1 & 0 & 0 \\
d & 0 & 1 & 0 & 0 \\
\end{array}
\]

Then swap the third row/column with the fourth row/column ($ b \leftrightarrow d $).

\[ A_G =\begin{array}{c|cccc}
 & a & c & d & b \\
\hline
a & 0 & 0 & 0 & 1 \\
c & 0 & 0 & 1 & 1 \\
d & 0 & 1 & 0 & 0 \\
b & 1 & 1 & 0 & 0 \\
\end{array}
\]

Now the adjacency matrix \( A_G \) matches the adjacency matrix \( A_H \).

\[ A_G =\begin{array}{c|cccc}
 & a & c & d & b \\
\hline
a & 0 & 0 & 0 & 1 \\
c & 0 & 0 & 1 & 1 \\
d & 0 & 1 & 0 & 0 \\
b & 1 & 1 & 0 & 0 \\
\end{array} = A_H = \begin{array}{c |cccc}
 & w & y & x & y \\
\hline
w & 0 & 0 & 0 & 1 \\
y & 0 & 0 & 1 & 1 \\
x & 0 & 1 & 0 & 0 \\
y & 1 & 1 & 0 & 0 \\
\end{array}
\]

This means that graphs \( G \) and \( H \) are isomorphic.

In other words, if we consider the permutation \( (a \rightarrow w, b \rightarrow y, c \rightarrow x, d \rightarrow z ) \), we see that \( A_G \) and \( A_H \) are identical.

This method is theoretically correct but can be computationally expensive because the number of permutations to consider grows factorially with the number of vertices (\( n! \)). Where \( n! \) is the factorial of \( n \).

For example, for a graph with \( n=4 \) vertices, there are \( 4!=24 \) permutations

$$ 4! = 4 \cdot 3 \cdot 2 \cdot 1 = 24 $$

But for a graph with \( n=5 \) vertices, there are \( 5!=120 \) permutations.

$$ 5! = 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 120 $$

And the situation becomes more challenging for larger graphs.

Comparing adjacency matrices by relabeling vertices is a valid method for verifying graph isomorphism. Although it can be inefficient for large graphs, it is useful for understanding the concept and applicable to smaller graphs. Alternatively, more efficient algorithms exist for checking graph isomorphism, such as the Weisfeiler-Lehman algorithm.

Properties of Isomorphic Graphs

When two graphs are isomorphic, their fundamental structural properties are preserved

This is crucial because isomorphism implies that graphs, although they may look different, are actually identical in their intrinsic structure.

Let's look in detail at some of these properties.

• Number of vertices and edges
  Two isomorphic graphs have the same number of vertices and the same number of edges. This is a direct consequence of the definition of isomorphism, which requires a bijective correspondence between the vertices that preserves the connections (edges).
• Vertex degree
  In two isomorphic graphs, each vertex has the same degree (number of incident edges). If a vertex \( v \) in \( G \) has degree \( k \), the corresponding vertex \( f(v) \) in \( H \) will also have degree \( k \).
• Subgraphs
  Any subgraph of an isomorphic graph corresponds to a subgraph of the other graph that is also isomorphic. In other words, the properties of the subgraphs are preserved.
• Cycles and paths
  Cycles (closed sequences of connected vertices) and paths (open sequences of connected vertices) in one graph have exact correspondences in the other graph. If there is a cycle of length \( k \) in \( G \), there will be a cycle of length \( k \) in \( H \).
• Connectivity
  The connectivity of a graph is preserved under isomorphism. If \( G \) is connected (i.e., there is a path between every pair of vertices), then \( H \) will be connected.
• Graph complement
  The complements of two isomorphic graphs are also isomorphic. The complement of a graph \( G \) is a graph where two vertices are connected if and only if they are not connected in \( G \).

The Isomorphism Relation Is an Equivalence Relation

To better understand, let's analyze the three main properties of equivalence relations: reflexivity, symmetry, and transitivity, in the context of isomorphic graphs.

1. Reflexive
   Every graph \( G \) is isomorphic to itself. This is true because the identity of the vertices and edges of \( G \) can be considered an isomorphism.
2. Symmetric
   If a graph \( G \) is isomorphic to a graph \( H \) (G≅H), then \( H \) is isomorphic to \( G \) (H≅G).
3. Transitive
   If a graph \( G \) is isomorphic to a graph \( H \) (G≅H), and \( H \) is isomorphic to a graph \( F \) (H≅F), then \( G \) is isomorphic to \( F \) (G≅F).

Therefore, isomorphic graphs form equivalence classes, where each class contains all graphs that are isomorphic to each other.