Cliques in Graph Theory
In graph theory, a clique refers to a subset of vertices within an undirected graph, each of which is directly connected to every other vertex in the subset.
This concept essentially describes a complete subgraph, where every possible vertex pair is linked by an edge, showcasing a perfect interconnectedness.
An Illustrative Example
Let's demystify the concept of cliques, maximal cliques, and the maximum clique with a straightforward example.
Consider a graph composed of five vertices named A, B, C, D, and E, interconnected as follows:
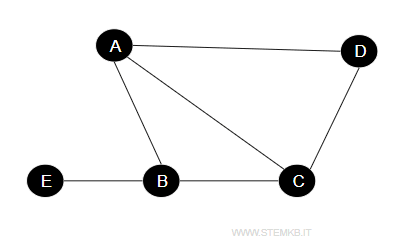
Upon review, the graph reveals several cliques.
For instance, the subset {A, B, C} qualifies as a clique since each vertex maintains direct connections with all others in the subset.
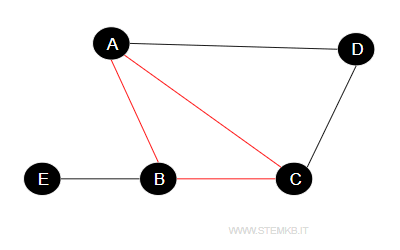
A single graph can feature multiple cliques, varying in size.
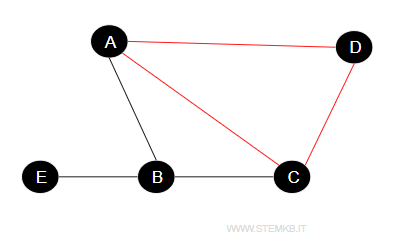
In our example, {A, C, D} represents another such clique.
At its most basic, any two adjacent vertices constitute a minimal clique. This property is illustrated when adjacent vertices, such as {E,B}, form a clique.
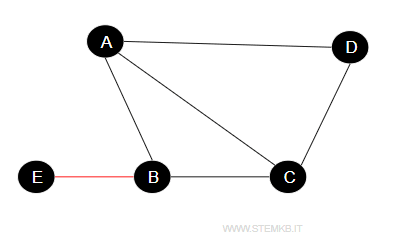
This principle applies uniformly to all pairs of adjacent vertices, including {A,B}, {A,C}, {A,D}, {B,C}, {C,D}.
However, the set {A,B,C,D} does not form a clique due to the lack of direct connection between B and D, illustrating that not all vertex subsets create cliques.

A maximal clique is identified when including any additional adjacent vertex disrupts the existing complete interconnectivity among the subset's vertices. Essentially, it signifies a subset that cannot be expanded without losing its clique status.
For instance, the subset {A, B, C} is a maximal clique as introducing any new vertex (such as D or E) would compromise the direct connectivity among all vertices in the subset.

Similarly, the subset {A, C, D} stands as another maximal clique.
Listing all maximal cliques in a graph can be daunting due to the potential exponential growth in the number of cliques relative to the graph's size.
The maximum clique is distinguished as the largest among all cliques within the graph, indicating the pinnacle of interconnectedness.
In the context of our example, both {A, B, C} and {A, C, D} are the largest cliques present, making them the maximum cliques by virtue of their three-vertex composition.

The significance of identifying the maximum clique extends beyond numerical value; it offers profound insights into the network's cohesion, revealing the deepest level of mutual connectivity among nodes.
The quest for the maximum clique presents a formidable computational challenge, classified as NP-complete, highlighting the absence of a polynomial-time solution applicable to all instances.
In the world of graph theory, the relationship between cliques and independent sets is deeply intertwined. These concepts serve as two sides of the same coin.
More concretely, each clique in a graph is mirrored by an independent set within its complementary graph, and vice versa, every independent set in the original framework emerges as a clique in its complement.
Take, for example, the clique consisting of vertices {A,B,C}; in the complement of the graph, this group transforms into an independent set.
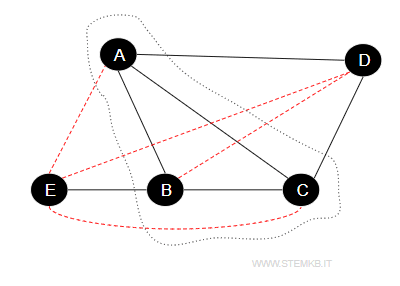
This elegant symmetry uncovers a deep-seated link between the notions of structural cohesion and independence within graphs. It highlights how the intricate web of connections can orchestrate contrasting dynamics in complementary scenarios.
Applications of Cliques
Exploring cliques within networks sheds light on the intricacies of complex systems, ranging from communication networks to scientific collaborations, and even social networking dynamics, enhancing our grasp of structural and functional patterns.

