Loops in Graph Theory

In the study of graphs, a loop is an edge that connects a vertex back to itself.

Considered a cycle of length one, loops originate from the concept that a cycle in graph theory is identified as a closed route where the start and end points are the same, without any repetition of vertices along the way.

Example

Take, for example, a computer network where each node represents a computer and each edge denotes a direct connection between two computers.

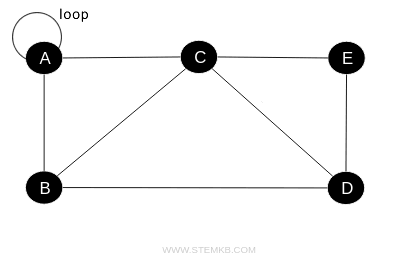
In this scenario, a loop could represent a computer connecting to itself, forming an internal feedback loop or a specific configuration designed for particular tasks.

This illustrates just one of the myriad ways in which graph theory can be applied to solve practical problems.

In an undirected graph, each loop increases the degree of its vertex by two, since for the purposes of degree calculation, a loop is counted as if the vertex were linked to itself twice. The degree of a vertex in such a graph is determined by the total number of edges incident to it, including loops. Therefore, if a vertex has n loops, each contributes twice to the degree of the vertex. Thus, if a vertex has \(n\) loops, each loop enhances the vertex's degree by 2. To be clear, if a vertex possesses a base degree \(d\) (namely, the count of edges excluding the loops) and \(n\) loops, then the vertex's aggregate degree equates to \(d + 2n\), rather than \(n + 2\). This calculation arises because each loop elevates the vertex's degree by a factor of 2. Consequently, if a vertex, say, harbors 3 loops, the loops' collective contribution to its degree would be \(2 \times 3 = 6\).

Consider another example.

When applying graph theory to a social network's architecture, where vertices signify users and edges represent connections like friendships or likes,

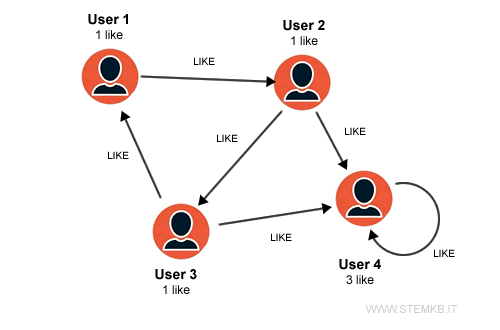
a loop might symbolize a user engaging with their own content, such as liking their own post or setting a personal reminder that only they can see within the platform.

This framework allows us to map and analyze social interactions on the platform, providing insights into user behavior through graph theory.

For instance, identifying loops and other patterns can reveal significant behaviors such as self-promotion or the management of personal content, crucial for understanding user engagement.

Graph theory, therefore, becomes an invaluable tool in dissecting and enhancing social dynamics, both in digital spaces and in real-world settings.

Graph Connectivity and Loops

The presence of a loop indicates that a vertex is connected back to itself through an edge, but this does not inherently suggest that the graph is connected.

A graph is deemed connected if there is a path linking every pair of vertices within it, ensuring that all parts of the graph are reachable from one another.

Hence, the connectivity of a graph is determined by the availability of paths between all vertex pairs, rather than by the existence of loops.

Example. To elucidate, consider a graph divided into two separate components: the first includes a vertex with a loop, and the second comprises several vertices without loops.

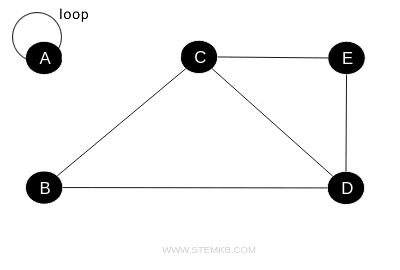
This graph is not considered connected because there is no pathway linking the vertices of the first component to those of the second, despite the loop in the first component.

One might mistakenly think of a vertex with a loop as being "connected to itself," yet this does not influence the overall connectivity of the graph in relation to other vertices.

Thus, assessing a graph's connectivity requires examining the paths that link all vertices, irrespective of the presence or absence of loops.