Simple Graphs

In the field of graph theory, the term simple graph refers to a distinct kind of graph, one devoid of loops and multiple edges.

Loops are defined as edges that connect a vertex back to itself, while multiple edges represent the existence of two or more connections between the same pair of vertices.

What sets simple graphs apart is their absence of these features, distinguishing them from multigraphs which might incorporate loops, multiple edges, or both.

An Illustrative Example

Consider a computer network to visualize a simple graph: in this network, each computer (or node) is connected to others through a singular network cable, each represented as an edge in the graph.

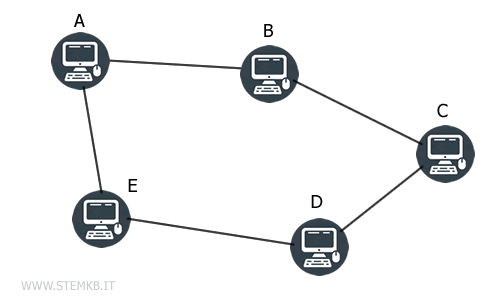
This framework makes it impractical to connect a computer to itself (avoiding loops) or to link two computers with more than one cable (avoiding multiple edges).

For example, linking computer A to itself with a cable is redundant. Similarly, connecting computer A to computer B with more than one cable serves no practical advantage. Such configurations, involving loops and multiple edges, do not contribute to utility in real-world applications.

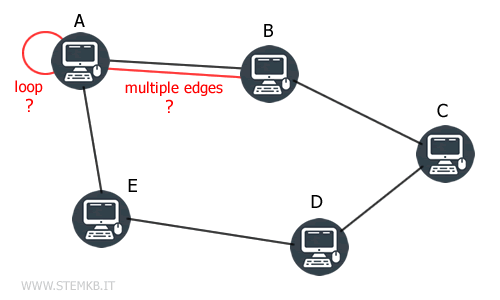
Therefore, the depiction of this network can be elegantly captured using a simple graph.

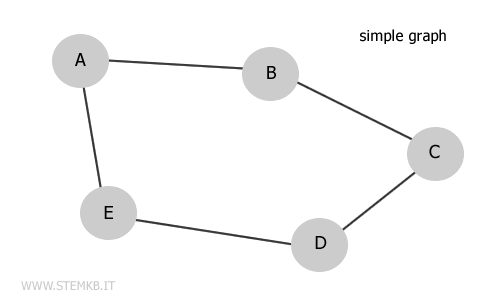
Thus, a simple graph serves as an ideal abstraction for modeling symmetric binary relationships between distinct entities, ensuring that any two entities are linked by no more than a single direct connection.

In the realm of simple graphs, an edge is defined as an unordered pair of distinct vertices, reflecting the bidirectional (or nondirectional) nature of the connection between vertices. Consequently, there’s no need to distinguish a direction or sequence for the two vertices that are linked.

This methodology simplifies how relationships are depicted by removing the requirement to specify vertex order within an edge or the orientation of connections within the graph.

Take, for instance, a simple graph where the edge connecting vertices \(A\) and \(B\) is represented as an unordered pair. Whether we express this as \(\{A, B\}\) or \(\{B, A\}\), or even \(AB\) or \(BA\), the underlying message is consistent: \(A\) and \(B\) are connected. This resembles the dynamics of friendship, where the relationship is reciprocal and doesn’t infer a direction or order in the pairing of \(A\) and \(B\).

By foregoing the formalities that often accompany the association of vertices to edges in a simple graph, attention can be more readily focused on the presence of connections between vertices, as opposed to the intricate details of these connections.

This characteristic renders simple graphs particularly adept at depicting networks and systems where redundant connections or internal links to a single component are either prohibited or irrelevant to the analysis being conducted. Here, the principal concern with relationships between pairs of objects is merely whether they exist.