Independent Sets in a Graph

An independent set (or stable set) is defined within a graph as a collection of vertices with no two directly connected by an edge.

To put it another way, there is no edge in the graph that links any two vertices from this set, ensuring they remain independent of each other.

This idea stands in contrast to a clique, characterized by every pair of vertices being adjacent within the subset.

An Illustrative Example

Imagine a straightforward graph consisting of five vertices: A, B, C, D, and E.

 

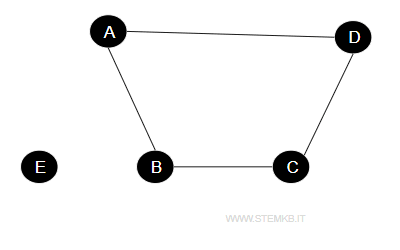
Within this graph, {B, D} forms an independent set as there is no direct connection between B and D.

Similarly, {A, C, E} also serves as an independent set, particularly noting that E isn’t linked to any other vertex.

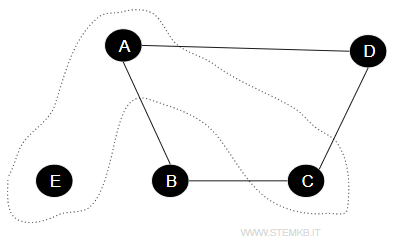
An independent set reaches a maximal status when adding any additional vertex would compromise its independence.

Take the set {A, C, E} for example; it's maximal because introducing another vertex (either D or B) would create a connection with at least one vertex already in the set, breaking the independent criterion.

A maximum independent set is the largest possible independent set a graph can accommodate.

For instance, {A, C, E} not only forms a maximal set but also qualifies as the maximum independent set, encompassing the highest number of vertices (3) without any of them being interconnected.

This represents the most extensive independent set feasible within the graph.

Identifying a maximum independent set poses an NP-hard challenge due to the lack of a universally efficient algorithm applicable to every graph type.

An interesting dynamic exists between independent sets and cliques in graph theory. Specifically, within the graph's complement, an independent set transforms into a clique and vice versa.

For example, converting our graph to its complement (illustrated with red lines) changes the independent set {A, C, E} into a clique.

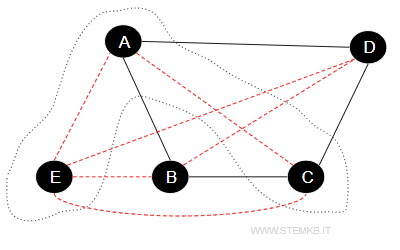
This interplay between independent sets and cliques allows for the rephrasing of clique-related issues as independent set problems and vice versa, providing a nuanced lens through which to examine the graph’s structure. However, it's critical to acknowledge that from a computational standpoint, finding a maximum set is as complex as locating a maximum clique within the graph’s complement.

Applications of Independent Sets

Independent sets are pivotal in solving resource allocation dilemmas where shared resources among adjacent projects or entities are not feasible.

In the context of scheduling, they depict tasks that can be executed concurrently without overlap or conflict.

Moreover, within social networking or market analysis realms, they can identify clusters of individuals or products without direct links or competition, offering valuable insights into effective marketing or networking strategies.