Graph Density

Graph density measures how well-connected the vertices of a graph are.

In an undirected graph \( G = (V, E) \) with \( n \) vertices and \( E \) edges, the density \( D \) is defined as the ratio of the actual number of edges \( E \) to the maximum possible number of edges between \( n \) vertices. The formula is:

\[ D = \frac{2E}{n(n-1)} \]

For directed graphs, the density \( D \) formula is slightly different:

\[ D = \frac{E}{n(n-1)} \]

Graph density ranges from 0 to 1. A density of 0 indicates a graph with no edges, while a density of 1 indicates a complete graph.

Why is density important?

Density is used to determine how close a graph is to being a complete graph.

The higher the density, the more interconnected the graph is.

It is a crucial measure for understanding the structure and connectivity of a network, useful in various fields such as social networks, computer science, and natural sciences. For instance, in social networks, density can indicate how tightly knit the network of relationships is. In communication networks, it can help evaluate the network's efficiency.

Practical Example

Consider an undirected graph with 5 vertices (A, B, C, D, E) and 6 edges.

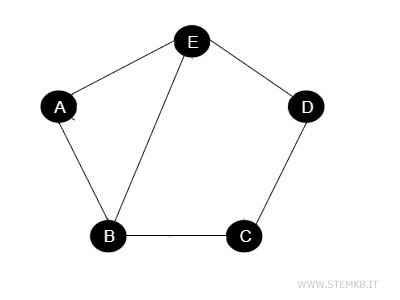
The density of this graph can be calculated as follows.

First, we calculate the maximum number of possible edges the graph can have.

$$ \frac{5(5-1)}{2} = 10 $$

Next, we apply the density formula.

$$ D = \frac{2 \cdot 6}{5(5-1)} = \frac{12}{20} = 0.6 $$

In this case, the graph's density is 0.6.

In other words, the graph is connected at 60% of its maximum potential.

The density of a graph increases linearly with the addition of edges. For example, if you add one more edge to the previous graph, the number of edges increases from 6 to 7, and the density goes from 0.6 to 0.7. Each added edge increases the graph's density by 0.1 because density is directly proportional to the number of edges relative to the maximum possible number of edges.