Relationship Between Vertex Connectivity, Edge Connectivity, and Minimum Degree in a Graph

The vertex connectivity $ \kappa(G) $ of a graph is always less than or equal to the edge connectivity $ \lambda(G) $, which, in turn, cannot exceed the minimum degree of the vertices $ \delta(G) $. $$ \kappa(G) \leq \lambda(G) \leq \delta(G) $$

This fundamental relationship in graph theory illustrates that:

Vertex connectivity ($ \kappa(G) $) is always less than or equal to edge connectivity ($ \lambda(G) $) because disconnecting a graph by removing vertices is typically more "costly" than by removing edges.
Edge connectivity ($ \lambda(G) $) is similarly capped by the minimum degree ($ \delta(G) $), as the vertex with the lowest degree sets a natural limit on how connectivity can be sustained through edges alone.

This inequality is a key concept, proving useful for analyzing a graph's structural strength or vulnerability.

A Practical Example

Let’s explore a simple example to clarify this relationship.

Imagine a graph $ G $ with five vertices: $ A $, $ B $, $ C $, $ D $, and $ E $, and six edges: $(A, B)$, $ (A, C)$, $ (B, C)$, $ (B, D)$, $ (B, E)$, $ (D, E)$.

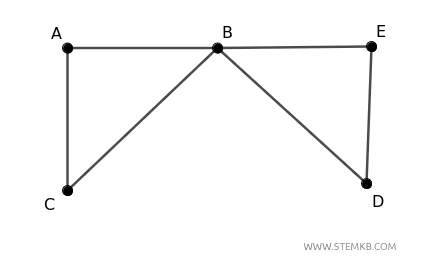
graph example

The vertex connectivity $ \kappa(G) $ of the graph is the minimum number of vertices that must be removed to disconnect it.

Here, removing vertex $ B $ results in two disconnected components.

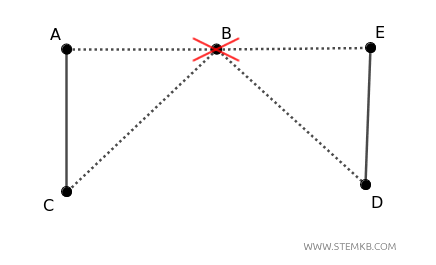
graph connectivity via vertices

Thus, the vertex connectivity $ \kappa(G) = 1 $, since removing just one vertex (either $ B $ or $ C $) disconnects the graph.

$$ \kappa(G) = 1 $$

Edge connectivity $ \lambda(G) $ represents the minimum number of edges that need to be removed to disconnect the graph.

In this case, by removing edges $(A, B)$ and $(B, C)$, the graph is split into two separate components: one containing vertices $ A $ and $ C $, and the other containing $ B $, $ D $, and $ E $.

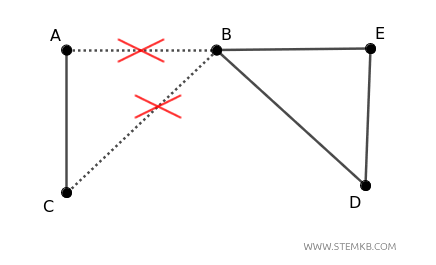
example

Thus, edge connectivity is $ \lambda(G) = 2 $, as at least two edges must be removed to disconnect the graph.

$$ \lambda(G) = 2 $$

The minimum degree $ \delta(G) $ is the lowest degree among all vertices in the graph.

In this case, the vertex degrees are:

$ \deg(A) = 2 $ (connected to $ B $ and $ C $),
$ \deg(B) = 4 $ (connected to $ A $, $ C $, $ D $, and $ E $),
$ \deg(C) = 2 $ (connected to $ A $ and $ B $),
$ \deg(D) = 2 $ (connected to $ B $ and $ E $).
$ \deg(E) = 2 $ (connected to $ B $ and $ D $).

Therefore, the minimum degree of the vertices in the graph is $ \delta(G) = 2 $.

$$ \delta(G) = 2 $$

Summing up, we find that $ \kappa(G) = 1 $, $ \lambda(G) = 2 $, and $ \delta(G) = 2 $.

This confirms the inequality $ \kappa(G) \leq \lambda(G) \leq \delta(G) $:

$$ 1 \leq 2 \leq 2 $$

This example illustrates that removing a single vertex is sufficient to disconnect the graph (vertex connectivity is 1).

However, to disconnect the graph by removing edges, at least two edges are needed (edge connectivity is 2).

The vertex with the fewest connections has a degree of 2, establishing a natural upper bound for edge connectivity.