Complement of a Graph

A graph complement refers to a graph that shares the same set of vertices with the original graph, yet it inverts the edge configuration: in this complementary graph, an edge connects two vertices if, and only if, such an edge was absent in the original graph.

Formally, the complement \( \bar{G} \) of a graph \( G \) consists of the same vertices $ V(G) $, but includes edges $ uv \in \bar{E}(G) $ that do not exist in the original graph $ uv \notin E(G) $.

This means that the complement graph essentially offers the reverse connectivity of the original graph.

If two vertices are not linked by an edge in the graph $ G $, they are connected in the complement \(  \bar{G} \) and the reverse is true as well.

The graph complement serves as a kind of reverse image in terms of vertex connections compared to the initial graph. It's akin to looking at the graph through a mirror.

Example

Consider a party scenario where a graph depicts the acquaintances among guests. Each guest represents a vertex, and a line (edge) is drawn between two guests if they are acquainted.

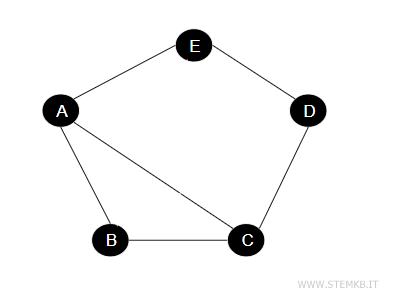
To create what could be termed an "anti-graph" of this social gathering, showing who is not acquainted with whom, we use the same vertices but draw lines exclusively between guests who have never met before.

As a result, every pair of guests lacking a connection in the initial graph now finds themselves connected in the complement, and vice versa.

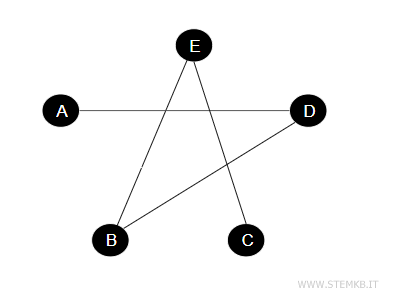
This so-called "anti-graph" is identified as the complement of the original graph. Essentially, it unveils all the absent connections from the original graph, offering a comprehensive perspective on potential interactions.

Interestingly, merging a graph \(G\) with its complement \( \bar{G} \) yields a complete graph. That's because in \(G\), certain vertices are interconnected, whereas in \( \bar{G} \), edges exist between all vertices not connected in \(G\). This amalgamation ensures that every vertex pair is interconnected, embodying the very essence of a complete graph. In such a graph, each vertex is directly connected to every other, leaving no pair unconnected.

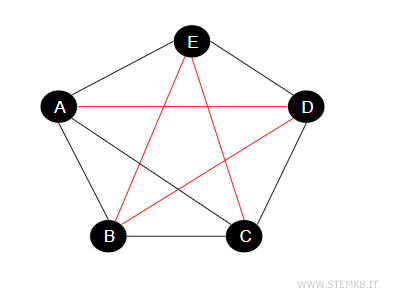
Studying a graph's complement opens up avenues for exploring the underlying properties of the original graph from a different angle.

At times, it proves simpler to deduce certain traits or characteristics from the complement rather than the graph itself.

Moreover, when tackling optimization problems like finding the maximum clique or the largest independent set, employing the graph's complement can streamline the process or enhance algorithmic efficiency.

For example, locating a maximal independent set in a graph directly corresponds to identifying a maximal clique in its complement.