Finite, Infinite, and Null Graphs

Graphs are classified by their vertices and edges into three key types: finite, infinite, and null graphs. Each represents unique features and applications.

Finite Graphs

Finite graphs have a specific number of vertices and edges. They're considered finite when both their sets of vertices (\(V\)) and edges (\(E\)) are countable. This characteristic allows for thorough exploration and analysis with a variety of algorithms and mathematical approaches. They are ideal for modeling tangible problems and processing through computational algorithms, such as Dijkstra's algorithm for finding the shortest path. For instance, a finite graph might include 5 vertices $ V=\{A,B,C,D,E\} $ and 7 edges $ E=\{AB,AC,BC,BD,CD,CE,ED\} $.

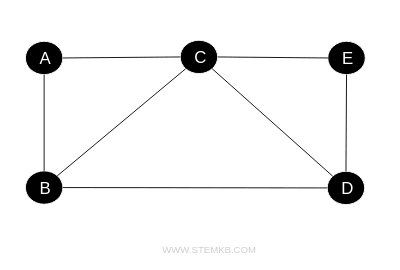
The finite nature allows for the use of algorithms to navigate paths, identify cycles, assess connectivity, and streamline routes. Moreover, it ensures that, with sufficient time and resources, these computational processes will conclude successfully. Finite graphs are utilized in various fields such as database management, computer networking, and algorithm development, to model and enhance data structures and communication flows. They also play a critical role in the design and analysis of transportation networks, electrical circuits, and control systems.

Infinite Graphs

Infinite graphs consist of an unlimited number of vertices and edges. They broaden the scope of graph theory to include systems without finite limits on nodes or connections. Infinite graphs pose greater analytical challenges and require distinct theoretical methodologies compared to their finite counterparts. They facilitate advanced mathematical exploration and the modeling of processes that are in constant expansion or iteration. Their significance in fields like mathematics and theoretical computer science lies in their ability to model structures or phenomena that are potentially limitless in scale or duration.

Infinite graphs have applications in areas such as number theory and mathematical logic. A well-known infinite graph is the integer graph, which connects each integer node to its immediate successors and predecessors, forming an endless sequence that stretches to both positive and negative infinity.

Null Graph

A null graph lacks both vertices and edges. It's defined by empty vertex (\(V\)) and edge (\(E\)) sets (\(V = \emptyset\) and \(E = \emptyset\)). Serving as a foundational element in graph theory, the null graph acts as a reference in various definitions and theorems. Despite its simplicity, the concept of a null graph plays a crucial role in formalizing certain graph properties and operations, laying the groundwork for more complex theories.

For instance, uniting a null graph with another does not alter the latter, akin to how adding zero to a number maintains its value.