A Bipartite Graph Has Even-Length Cycles

A graph $ G $ is bipartite if and only if every cycle in $ G $ has an even length.

A graph is a set of vertices connected by edges.

A graph is bipartite if we can divide its vertices into two disjoint sets $ A $ and $ B $ such that every edge connects a vertex in $ A $ with a vertex in $ B $.

In other words, there are no edges connecting two vertices within the same set $ A $ or $ B $.

Example
Proof

Example

Let's clarify this concept with a practical example.

Suppose we have a graph with the following vertices and edges:

Vertices: $ \{A, B, C, D, E, F\} $
Edges: $ \{(A, B), (A, D), (B, C), (C, D), (D, E), (E, F)\} $

Let's divide the vertices into two sets $ X = \{A, C, E\} $ and $ Y = \{B, D, F\} $ so that every edge connects a vertex in $ X $ with a vertex in $ Y $.

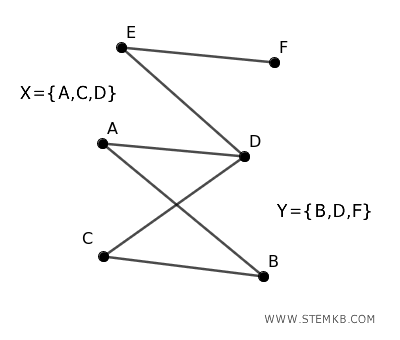
example of bipartite graph

We will verify each edge one by one:

(A, B) → $ A $ is in $ X $ and $ B $ is in $ Y $
(A, D) → $ A $ is in $ X $ and $ D $ is in $ Y $
(B, C) → $ B $ is in $ Y $ and $ C $ is in $ X $
(C, D) → $ C $ is in $ X $ and $ D $ is in $ Y $
(D, E) → $ D $ is in $ Y $ and $ E $ is in $ X $
(E, F) → $ E $ is in $ X $ and $ F $ is in $ Y $

Each edge connects a vertex in $ X $ with a vertex in $ Y $, hence the graph is bipartite.

Now let's examine the cycle $ A \to B \to C \to D \to A $ in this graph.

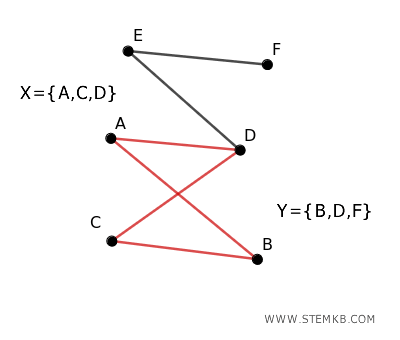
the cycle is of even length

We will analyze the edges one by one:

A → B: A is in $ X $, B is in $ Y $
B → C: B is in $ Y $, C is in $ X $
C → D: C is in $ X $, D is in $ Y $
D → A: D is in $ Y $, A is in $ X $

The cycle has a length of 4, which is even.

Example of a Non-Bipartite Graph

Now consider a graph with vertices $ \{P, Q, R, S\} $ and edges $ \{(P, Q), (Q, R), (R, S), (S, P), (P, R)\} $.

Let's try to divide the vertices into two sets $ X = \{P, R\} $ and $ Y = \{Q, S\} $:

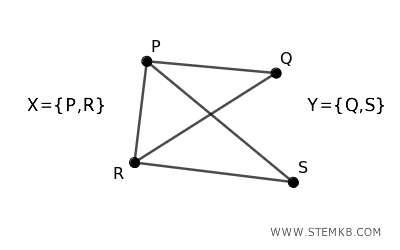
non-bipartite graph

We will verify the edges:

(P, Q) → $ P $ is in $ X $ and $ Q $ is in $ Y $
(Q, R) → $ Q $ is in $ Y $ and $ R $ is in $ X $
(R, S) → $ R $ is in $ X $ and $ S $ is in $ Y $
(S, P) → $ S $ is in $ Y $ and $ P $ is in $ X $
(P, R) → $ P $ is in $ X $ and $ R $ is in $ X $, which causes a problem because both are in the same set

In this graph, we have the edge (P, R) that connects two vertices within the same set $ X $, so the graph is not bipartite.

In fact, this graph contains odd-length cycles. For example, $ P \to Q \to R \to P $, where the starting and ending vertices are the same and counted once.

The presence of an odd cycle, even alongside even cycles, indicates that the graph cannot be bipartite. For instance, if we add the edge (Q, S) to the graph, we introduce an even-length cycle $ P \to Q \to S \to R \to P $. However, the presence of odd cycles like PQR and PRS shows that the graph is not bipartite.
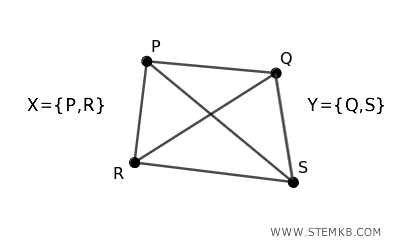
example of non-bipartite graph with an even-length cycle

In conclusion, a graph is bipartite if we can divide its vertices into two sets such that every edge connects a vertex in one set with a vertex in the other set.

In this case, every cycle in the graph will have an even length. If there is even one odd-length cycle, the graph cannot be bipartite.

Proof

The proof is divided into two parts:

Part 1: If $ G $ is bipartite, then every cycle has an even length.

If $ G $ is bipartite, we can divide the vertices into two sets $ A $ and $ B $ such that every edge connects a vertex in $ A $ with one in $ B $.

Suppose we have a cycle $ v_0 \to v_1 \to \ldots \to v_n \to v_0 $.

Assume $ v_0 $ is in $ A $. Then:

$ v_1 $ will be in $ B $
$ v_2 $ will be in $ A $
$ v_3 $ will be in $ B $
and so on...

Since $ v_n $ must be in $ B $ and then return to $ v_0 $ in $ A $, the number of steps (or edges) in the cycle must be even.

Thus, the cycle has an even length.

Part 2: If every cycle has an even length, then $ G $ is bipartite.

Assume every cycle in $ G $ has an even length.

Choose a vertex $ v $ and define two sets:

$ A $: set of vertices $ w $ where the shortest path from $ v $ to $ w $ has an even length.
$ B $: set of vertices $ w $ where the shortest path from $ v $ to $ w $ has an odd length.

If two vertices in $ A $ were adjacent, there would be an odd-length cycle (the path from $ v $ to each of the two vertices plus the edge between them).

Since every cycle has an even length, there cannot be two adjacent vertices in $ A $, and the same applies to $ B $.

Therefore, every edge must connect a vertex in $ A $ with a vertex in $ B $, which means $ G $ is bipartite.

Conclusion

A graph is bipartite if and only if every cycle in the graph has an even length.

This means we can divide the vertices of the graph into two sets such that every edge connects vertices from different sets, and if there is a cycle in this graph, it must have an even number of edges.

A Bipartite Graph Has Even-Length Cycles

Example

Example of a Non-Bipartite Graph

Proof

Part 1: If \( G \) is bipartite, then every cycle has an even length.

Part 2: If every cycle has an even length, then \( G \) is bipartite.

Conclusion