Do Loops in a Graph Match the Count of Vertices with Odd Degrees?
No, this notion is off the mark. There's no direct correlation between the number of loops in a graph and the count of vertices with odd degrees.
Such confusion likely arises from misconceptions about the basics of graph theory.
Let's demystify these concepts with real-world examples to enhance understanding.
- Loops: A loop is essentially an edge that connects a vertex back to itself. Each loop effectively doubles the degree of its vertex, as it counts each endpoint of the edge separately towards the vertex’s degree.
- Vertices with Odd Degrees: A vertex's degree — the total tally of edges connecting it to the graph, with loops counting as two — can land on either even or odd numbers. This total is influenced by all connecting edges, not just loops.
The Handshaking Lemma, a fundamental principle of graph theory, assures us that any graph will feature an even number of vertices with odd degrees.
Yet, this principle does not link the quantity of loops to the odd-degree vertices directly.
Illustrative Example
Take, for instance, a graph consisting solely of one vertex and a loop:
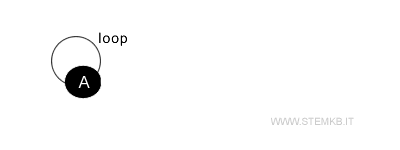
In this scenario, we're looking at a single vertex (A) sporting a degree of 2 — thanks to the loop's dual contribution.
Despite having an odd number of loops (1), this graph doesn't feature any vertices with odd degrees, clearly debunking the initial claim.
Now, consider another scenario for clarity.
A graph with three vertices, where two (B and C) are linked by an edge and the third (A) is adorned with a loop.
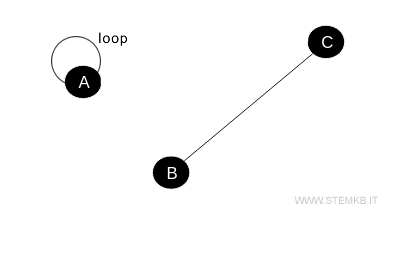
Here, vertex A with the loop is counted as having a degree of 2, while B and C each have a degree of 1, courtesy of their single connecting edge.
This setup results in two vertices with odd degrees, yet there's only one loop present — further discrediting the initial assumption.
To wrap up, the presence of loops in a graph doesn't dictate the presence or absence of vertices with odd degrees.
Hopefully, these examples have helped untangle any confusion.

